الطول الموجي لدي برولي

 أن للإشعاع الكهرومغناطيسي طبيعة مزودة. فهو يحمل خصائص موجية تجعله يظهر تأثيرات التداخل والحيود. كما أن له سلوك الجسيمات كما يتضح من خواصه الفوتونية. ومن الطبيعي في وجود هذه الثنائية أن نتكهن أن الإلكترون، وربما جسيمات اخرى، خواص موجية.

وبالفعل، كان لويس دي برولي أول من اقترح ــ بجدية ــ الطبيعة المزدوجة للإلكترون. وكان من بين ما دفعه إلى اقتراحه ذلك، النظرية الموجية لنيلز بوهر حول ذرة الهيدروجين. فقد اكتشف دي برولي عام 1923 أنه يستطيع تبرير أحد فروض بوهر الرئيسية تبريراً منطقياً إذا اعتبر أن الإلكترون خواص موجية. وسوف نقفز مباشرة إلى نتيجة دي برولي بدلاً من الغواص في الأحداث التاريخية التي أدت إليها.

إن كمية تحرك الفوتون ــ كما رأينا ــ هي h/c ولذلك فإن طوله الموجي هو  = h/p_photonλ وبالمثل ، فإذا كان لجسيم ما خواص موجية، فقد يرتبط الطول الموجي المصاحب له وكذا كمية تحركه بمعادلة شبيهة بهذه. وقد افترض دي برولي أن للجسيمات خواص موجية وأن طولها الموجي هو

(1)    

حيث h هو ثابت بلانك و p كمية تحرك الجسيم المعني.

وقد قام البرهان على صحة افتراض دي برولي تجريبياً بطريقة الصدفة على أيدي س. ج دافيسون و ل. هـ. جيرمر عام 1927. لقد كانا يبحثان في تطاير حزمة من الإلكترون عند سقوطها على بلورة فلزية (النيكل). ويصور الشكل 1)) رسماً تخطيطياً للجهاز الذي استخدماه وكان بداخل غرفة مفرغة. وكانت التجربة تبدأ بتعجيل حزمة من الإلكترون عن طريق إكسابها طاقة عند عبورها في فرق جهد كهربي V. ثم كانت القياسات تجرى لمعرفة عدد الإلكترونات المتطايرة من سطح البلورة عندما تسقط عليها الحزمة. وكانت النتيجة غير المتوقعة لهذه التجربة أن الإلكترون كانت تتطاير بقوة عند زوايا خاصة معينة فقط. وحينئذ لم يتمكن دافيسون وجيرمر من تفسير ذلك.

ثم تقدم بعضهم باقتراح إلى الباحثين بأن تلك النتيجة قد تكون برهاناً لأفكار دي برولي. وعندئذ عكف الاثنان على مزيد من القياسات مستخدمين بلورات تم توجيهها بشكل صحيح لمعرفة ما إذا كانت الزوايا المحددة بكل وضوح الإلكترون المتطايرة قابلة للتفسير في ضوء ظواهر التداخل التي تنشأ عن المسافات المنتظمة بين صفوف الذرات داخل البلورة والتي تؤدي دور محزوز للحيود ذي نوع خاص وجدير بالذكر هنا  الفيزيائيين و. هـ براج وابنه و. ل براج قد وضعا نظرية حيود أشعة إكس بواسطة البلورات عام 1913؛ وكان ذلك أساساً لعلم البلورات باستخدام أشعة إكس والذي يرجع إليه الفضل في معرفة تركيب البلورات والجزيئات المعقدة مثل جزئ DNA.

إذا كانت المسافة بين مستويات بلورة ما هي d، وكان الطول الموجي هو λ، فإن انعكاساً قوياً (تداخل بناء) لابد أن يقع عند الزوايا التي تعطى بالعلاقة

  λ = 2d sin θ_m                   m = 1, 2, 3,…   m

حيث θ في هذه الحالة هي الزاوية بين الحزمة المتطايرة ومستوى التشتت (التطاير)، والمسافة d في معظم البلورات من رتبة 0.1 nm. ولعلك تذكر أن ظواهر التداخل تتجلى فقط عندما يكون الطول الموجي للضوء الساقط له نفس تباعد المحزوز تقريباً. وعندئذ لابد لحدوث حيود بالبلورة أن يكون الطول الموجي 0.1nm بالتقريب، وهو ما يقع في منطقة أشعة إكس من الطيف الكهرومغناطيسي.

الشكل 1)): قاس دافيسون وجيرمر أعداد الإلكترونات المنعكسة من البلورة عند زوايا مختلفة.

وحيث أن دافيسون وجيرمر كانا يعرفنا قيمة d وقاسا مواقع الانعكاس القوى θ للإلكترونات فإنهما تمكنا من حساب λ ومن ناحية أخرى، حيث أن mv² = Ve½، فإنهما استطاعا حساب كمية تحرك الإلكترونات:

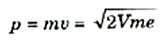
حيث V هو فرق الجهد الكهربي الذي تعجل من خلاله حزمة الإلكترونات، ومن هذه القيمة تمكن دافيسون وجيرمر من إيجاد الطول الموجي لدى برولي مرة ثانية،  = h/pλ ؛ ووجد أن قيمتي λ متطابقتان. وبعبارة أخرى، تنعكس الإلكترونات بنفس الطريقة التي لابد أن تنعكس بها موجات دي برولي المصاحبة لها. وهذا هو البرهان المباشر لفكرة دي برولي من أن للإلكترونات خواص موجية.

مواضيع ذات صلة

ميكانيكا الكم الخاصة بالروابط

ما الفائدة؟

إعادة النظر في اللامحلية

عوالم متعدّدة

هل نغيّر الفيزياء؟

الاحتمالات والقياسات

مبرهنة بيل وضرورة اللامحلية

الترابط والتشابك

الحالات الكمية والتراكب الكمي

التداخل والقياس

ألغاز الكم

Equipartition and the quantum oscillator