First, we know that a gas exerts a pressure, and we must clearly understand what this is due to. If our ears were a few times more sensitive, we would hear a perpetual rushing noise. Evolution has not developed the ear to that point, because it would be useless if it were so much more sensitive—we would hear a perpetual racket. The reason is that the eardrum is in contact with the air, and air is a lot of molecules in perpetual motion and these bang against the eardrums. In banging against the eardrums, they make an irregular tattoo—boom, boom, boom—which we do not hear because the atoms are so small, and the sensitivity of the ear is not quite enough to notice it. The result of this perpetual bombardment is to push the drum away, but of course there is an equal perpetual bombardment of atoms on the other side of the eardrum, so the net force on it is zero. If we were to take the air away from one side, or change the relative amounts of air on the two sides, the eardrum would then be pushed one way or the other, because the amount of bombardment on one side would be greater than on the other. We sometimes feel this uncomfortable effect when we go up too fast in an elevator or an airplane, especially if we also have a bad cold (when we have a cold, inflammation closes the tube which connects the air on the inside of the eardrum with the outside air through the throat, so that the two pressures cannot readily equalize).
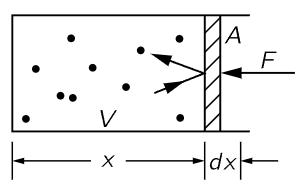
Fig. 39–1. Atoms of a gas in a box with a frictionless piston.
In considering how to analyze the situation quantitatively, we imagine that we have a volume of gas in a box, at one end of which is a piston which can be moved (Fig. 39–1). We would like to find out what force on the piston results from the fact that there are atoms in this box. The volume of the box is V, and as the atoms move around inside the box with various velocities they bang against the piston. Suppose there is nothing, a vacuum, on the outside of the piston. What of it? If the piston were left alone, and nobody held onto it, each time it got banged it would pick up a little momentum and it would gradually get pushed out of the box. So in order to keep it from being pushed out of the box, we have to hold it with a force F. The problem is, how much force? One way of expressing the force is to talk about the force per unit area: if A is the area of the piston, then the force on the piston will be written as a number times the area. We define the pressure, then, as equal to the force that we have to apply on a piston, divided by the area of the piston:
P=F/A. (39.1)
To make sure we understand the idea (we have to derive it for another purpose anyway), the differential work dW done on the gas in compressing it by moving the piston in a differential amount −dx would be the force times the distance that we compress it, which, according to (39.1), would be the pressure times the area, times the distance, which is equal to minus the pressure times the change in the volume:
dW=F(−dx)=−PAdx=−PdV. (39.2)
(The area A times the distance dx is the volume change.) The minus sign is there because, as we compress it, we decrease the volume; if we think about it we can see that if a gas is compressed, work is done on it.
How much force do we have to apply to balance the banging of the molecules? The piston receives from each collision a certain amount of momentum. A certain amount of momentum per second will pour into the piston, and it will start to move. To keep it from moving, we must pour back into it the same amount of momentum per second from our force. Of course, the force is the amount of momentum per second that we must pour in. There is another way to put it: if we let go of the piston it will pick up speed because of the bombardments; with each collision we get a little more speed, and the speed thus accelerates. The rate at which the piston picks up speed, or accelerates, is proportional to the force on it. So we see that the force, which we already have said is the pressure times the area, is equal to the momentum per second delivered to the piston by the colliding molecules.
To calculate the momentum per second is easy—we can do it in two parts: first, we find the momentum delivered to the piston by one particular atom in a collision with the piston, then we have to multiply by the number of collisions per second that the atoms have with the wall. The force will be the product of these two factors. Now let us see what the two factors are: In the first place, we shall suppose that the piston is a perfect “reflector” for the atoms. If it is not, the whole theory is wrong, and the piston will start to heat up and things will change, but eventually, when equilibrium has set in, the net result is that the collisions are effectively perfectly elastic. On the average, every particle that comes in leaves with the same energy. So we shall imagine that the gas is in a steady condition, and we lose no energy to the piston because the piston is standing still. In those circumstances, if a particle comes in with a certain speed, it comes out with the same speed and, we will say, with the same mass.
If v is the velocity of an atom, and vx is the x-component of v, then mvx is the x-component of momentum “in”; but we also have an equal component of momentum “out,” and so the total momentum delivered to the piston by the particle, in one collision, is 2mvx, because it is “reflected.”
Now, we need the number of collisions made by the atoms in a second, or in a certain amount of time dt; then we divide by dt. How many atoms are hitting? Let us suppose that there are N atoms in the volume V, or n=N/V in each unit volume. To find how many atoms hit the piston, we note that, given a certain amount of time t, if a particle has a certain velocity toward the piston it will hit during the time t, provided it is close enough. If it is too far away, it goes only part way toward the piston in the time t, but does not reach the piston. Therefore, it is clear that only those molecules which are within a distance vxt from the piston are going to hit the piston in the time t. Thus the number of collisions in a time t is equal to the number of atoms which are in the region within a distance vxt, and since the area of the piston is A, the volume occupied by the atoms which are going to hit the piston is vxtA. But the number of atoms that are going to hit the piston is that volume times the number of atoms per unit volume, nvxtA. Of course, we do not want the number that hit in a time t, we want the number that hit per second, so we divide by the time t, to get nvxA. (This time t could be made very short; if we feel we want to be more elegant, we call it dt, then differentiate, but it is the same thing.)
So we find that the force is
F=nvxA⋅2mvx. (39.3)
See, the force is proportional to the area, if we keep the particle density fixed as we change the area! The pressure is then
P=2nmv2x. (39.4)
Now we notice a little trouble with this analysis: First, all the molecules do not have the same velocity, and they do not move in the same direction. So, all the v2x’s are different! So what we must do, of course, is to take an average of the v2x’s, since each one makes its own contribution. What we want is the square of vx, averaged over all the molecules:
P=nm⟨v2x⟩. (39.5)
Did we forget to include the factor 2? No; of all the atoms, only half are headed toward the piston. The other half are headed the other way, so the number of atoms per unit volume that are hitting the piston is only n/2.
Now as the atoms bounce around, it is clear that there is nothing special about the “x-direction”; the atoms may also be moving up and down, back and forth, in and out. Therefore, it is going to be true that ⟨v2x⟩, the average motion of the atoms in one direction, and the average in the other two directions, are all going to be equal:
⟨v2x⟩=⟨v2y⟩=⟨v2z⟩. (39.6)
It is only a matter of rather tricky mathematics to notice, therefore, that they are each equal to one-third of their sum, which is of course the square of the magnitude of the velocity:
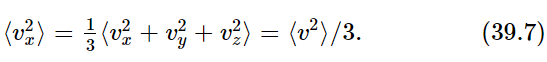
This has the advantage that we do not have to worry about any particular direction, and so we write our pressure formula again in this form:

The reason we wrote the last factor as ⟨mv2/2⟩ is that this is the kinetic energy of the center-of-mass motion of the molecule. We find, therefore, that
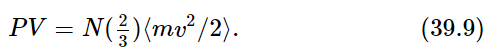
With this equation we can calculate how much the pressure is, if we know the speeds.
As a very simple example let us take helium gas, or any other gas, like mercury vapor, or potassium vapor of high enough temperature, or argon, in which all the molecules are single atoms, for which we may suppose that there is no internal motion in the atom. If we had a complex molecule, there might be some internal motion, mutual vibrations, or something. We suppose that we may disregard that; this is actually a serious matter that we will have to come back to, but it turns out to be all right. We suppose that the internal motion of the atoms can be disregarded, and therefore, for this purpose, that the kinetic energy of the center-of-mass motion is all the energy there is. So, for a monatomic gas, the kinetic energy is the total energy. In general, we are going to call U the total energy (it is sometimes called the total internal energy—we may wonder why, since there is no external energy to a gas), i.e., all the energy of all the molecules in the gas, or the object, whatever it is.
For a monatomic gas we will suppose that the total energy U is equal to a number of atoms times the average kinetic energy of each, because we are disregarding any possibility of excitation or motion inside the atoms themselves. Then, in these circumstances, we would have

Incidentally, we can stop here and find the answer to the following question: Suppose that we take a can of gas and compress the gas slowly, how much pressure do we need to squeeze the volume down? It is easy to find out, since the pressure is 2/3 the energy divided by V. As we squeeze it down, we do work on the gas and we thereby increase the energy U. So we are going to have some kind of a differential equation: If we start out in a given circumstance with a certain energy and a certain volume, we then know the pressure. Now we start to squeeze, but the moment we do, the energy U increases and the volume V decreases, so the pressure goes up.
So, we have to solve a differential equation, and we will solve it in a moment. We must first emphasize, however, that as we are compressing this gas, we are supposing that all the work goes into increasing the energy of the atoms inside. We may ask, “Isn’t that necessary? Where else could it go?” It turns out that it can go another place. There are what we call “heat leaks” through the walls: the hot (i.e., fast-moving) atoms that bombard the walls, heat the walls, and energy goes away. We shall suppose for the present that this is not the case.
For somewhat wider generality, although we are still making some very special assumptions about our gas, we shall write, not PV=2/3 U, but

It is written (γ−1) times U for conventional reasons, because we will deal with a few other cases later where the number in front of U will not be 2/3, but will be a different number. So, in order to do the thing in general, we call it γ−1, because people have been calling it that for almost one hundred years. This γ, then, is 5/3 for a monatomic gas like helium, because 5/3−1 is 2/3.
We have already noticed that when we compress a gas the work done is −PdV. A compression in which there is no heat energy added or removed is called an adiabatic compression, from the Greek a (not) + dia (through) + bainein (to go). (The word adiabatic is used in physics in several ways, and it is sometimes hard to see what is common about them.) That is, for an adiabatic compression all the work done goes into changing the internal energy. That is the key—that there are no other losses of energy—for then we have PdV=−dU. But since U=PV/(γ−1), we may write

Fortunately, assuming that γ is constant, as it is for a monatomic gas, we can integrate this: it gives γlnV+lnP=lnC, where lnC is the constant of integration. If we take the exponential of both sides, we get the law

In other words, under adiabatic conditions, where the temperature rises as we compress because no heat is being lost, the pressure times the volume to the 5/3 power is a constant for a monatomic gas! Although we derived it theoretically, this is, in fact, the way monatomic gases behave experimentally.
 الاكثر قراءة في خواص المادة
الاكثر قراءة في خواص المادة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


