
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
The specific heats of gases
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 40
2024-05-23
939
Now we shall look at some ways to test the theory, and to see how successful is the classical theory of gases. We saw earlier that if U is the internal energy of N molecules, then PV= NkT= (γ−1)U holds, sometimes, for some gases, maybe. If it is a monatomic gas, we know this is also equal to 2/3 of the kinetic energy of the center-of-mass motion of the atoms. If it is a monatomic gas, then the kinetic energy is equal to the internal energy, and therefore γ−1=2/3. But suppose it is, say, a more complicated molecule, that can spin and vibrate, and let us suppose (it turns out to be true according to classical mechanics) that the energies of the internal motions are also proportional to kT. Then at a given temperature, in addition to kinetic energy 3/2 kT, it has internal vibrational and rotational energies. So the total U includes not just the kinetic energy, but also the rotational and vibrational energies, and we get a different value of γ. Technically, the best way to measure γ is by measuring the specific heat, which is the change in energy with temperature. We will return to that approach later. For our present purposes, we may suppose γ is found experimentally from the PVγ curve for adiabatic compression.
Let us make a calculation of γ for some cases. First, for a monatomic gas U is the total energy, the same as the kinetic energy, and we know already that γ should be 5/3. For a diatomic gas, we may take, as an example, oxygen, hydrogen iodide, hydrogen, etc., and suppose that the diatomic gas can be represented as two atoms held together by some kind of force like the one of Fig. 40–3.
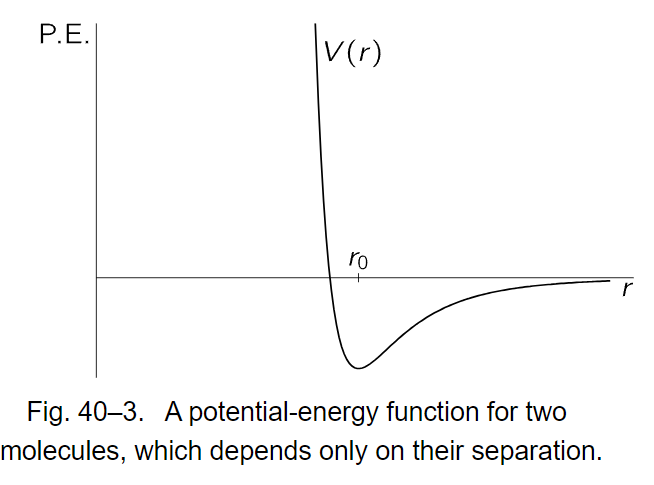
We may also suppose, and it turns out to be quite true, that at the temperatures that are of interest for the diatomic gas, the pairs of atoms tend strongly to be separated by r0, the distance of potential minimum. If this were not true, if the probability were not strongly varying enough to make the great majority sit near the bottom, we would have to remember that oxygen gas is a mixture of O2 and single oxygen atoms in a nontrivial ratio. We know that there are, in fact, very few single oxygen atoms, which means that the potential energy minimum is very much greater in magnitude than kT, as we have seen. Since they are clustered strongly around r0, the only part of the curve that is needed is the part near the minimum, which may be approximated by a parabola. A parabolic potential implies a harmonic oscillator, and in fact, to an excellent approximation, the oxygen molecule can be represented as two atoms connected by a spring.
Now what is the total energy of this molecule at temperature T? We know that for each of the two atoms, each of the kinetic energies should be 3/2 kT, so the kinetic energy of both of them is 3/2 kT+3/2 kT. We can also put this in a different way: the same 3/2 plus 3/2 can also be looked at as kinetic energy of the center of mass (3/2), kinetic energy of rotation (2/2), and kinetic energy of vibration (1/2). We know that the kinetic energy of vibration is 1/2, since there is just one dimension involved and each degree of freedom has 1/2 kT. Regarding the rotation, it can turn about either of two axes, so there are two independent motions. We assume that the atoms are some kind of points, and cannot spin about the line joining them; this is something to bear in mind, because if we get a disagreement, maybe that is where the trouble is. But we have one more thing, which is the potential energy of vibration; how much is that? In a harmonic oscillator the average kinetic energy and average potential energy are equal, and therefore the potential energy of vibration is 1/2 kT, also. The grand total of energy is U=7/2 kT, or kT is 2/7 U per atom. That means, then, that γ is 9/7 instead of 5/3, i.e., γ=1.286.
We may compare these numbers with the relevant measured values shown in Table 40–1. Looking first at helium, which is a monatomic gas, we find very nearly 5/3, and the error is probably experimental, although at such a low temperature there may be some forces between the atoms. Krypton and argon, both monatomic, agree also within the accuracy of the experiment.
Table 40–1
Values of the specific heat ratio, γ
, for various gases
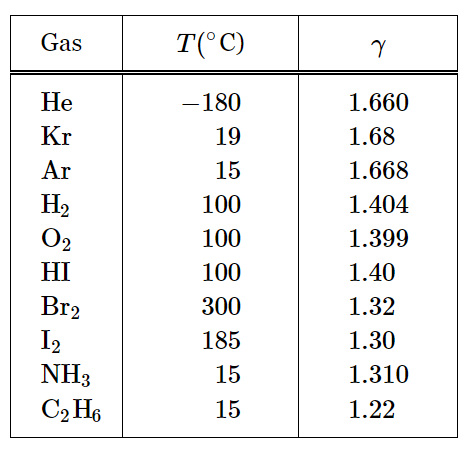
We turn to the diatomic gases and find hydrogen with 1.404, which does not agree with the theory, 1.286. Oxygen, 1.399, is very similar, but again not in agreement. Hydrogen iodide again is similar at 1.40. It begins to look as though the right answer is 1.40, but it is not, because if we look further at bromine we see 1.32, and at iodine we see 1.30. Since 1.30 is reasonably close to 1.286, iodine may be said to agree rather well, but oxygen is far off. So here we have a dilemma. We have it right for one molecule, we do not have it right for another molecule, and we may need to be pretty ingenious in order to explain both.
Let us look further at a still more complicated molecule with large numbers of parts, for example, C2H6, which is ethane. It has eight different atoms, and they are all vibrating and rotating in various combinations, so the total amount of internal energy must be an enormous number of kT’s, at least 1/2 kT for kinetic energy alone, and γ−1 must be very close to zero, or γ almost exactly 1. In fact, it is lower, but 1.22 is not so much lower, and is higher than the 1112 calculated from the kinetic energy alone, and it is just not understandable!
Furthermore, the whole mystery is deep, because the diatomic molecule cannot be made rigid by a limit. Even if we made the couplings stiffer indefinitely, although it might not vibrate much, it would nevertheless keep vibrating. The vibrational energy inside is still kT, since it does not depend on the strength of the coupling. But if we could imagine absolute rigidity, stopping all vibration to eliminate a variable, then we would get U=5/2 kT and γ=1.40 for the diatomic case. This looks good for H2 or O2. On the other hand, we would still have problems, because γ for either hydrogen or oxygen varies with temperature! From the measured values shown in Fig. 40–6, we see that for H2, γ varies from about 1.6 at −185∘C to 1.3 at 2000∘C. The variation is more substantial in the case of hydrogen than for oxygen, but nevertheless, even in oxygen, γ tends definitely to go up as we go down in temperature.
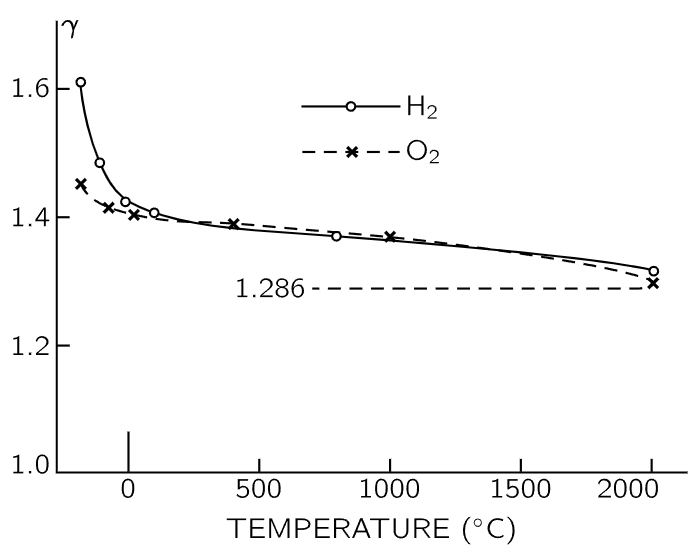
Fig. 40–6. Experimental values of γ as a function of temperature for hydrogen and oxygen. Classical theory predicts γ=1.286, independent of temperature.