
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
The random walk
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 41
2024-06-03
2001
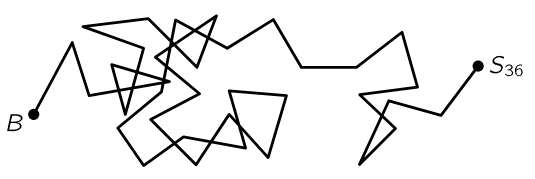
Fig. 41–6. A random walk of 36 steps of length l. How far is S36 from B? Ans: about 6l on the average.
Let us consider how the position of a jiggling particle should change with time, for very long times compared with the time between “kicks.” Consider a little Brownian movement particle which is jiggling about because it is bombarded on all sides by irregularly jiggling water molecules. Query: After a given length of time, how far away is it likely to be from where it began? This problem was solved by Einstein and Smoluchowski. If we imagine that we divide the time into little intervals, let us say a hundredth of a second or so, then after the first hundredth of a second it moves here, and in the next hundredth it moves some more, in the next hundredth of a second it moves somewhere else, and so on. In terms of the rate of bombardment, a hundredth of a second is a very long time. The reader may easily verify that the number of collisions a single molecule of water receives in a second is about 1014, so in a hundredth of a second it has 1012 collisions, which is a lot! Therefore, after a hundredth of a second it is not going to remember what happened before. In other words, the collisions are all random, so that one “step” is not related to the previous “step.” It is like the famous drunken sailor problem: the sailor comes out of the bar and takes a sequence of steps, but each step is chosen at an arbitrary angle, at random (Fig. 41–6). The question is: After a long time, where is the sailor? Of course we do not know! It is impossible to say. What do we mean—he is just somewhere more or less random. Well then, on the average, where is he? On the average, how far away from the bar has he gone? We have already answered this question, because once we were discussing the superposition of light from a whole lot of different sources at different phases, and that meant adding a lot of arrows at different angles. There we discovered that the mean square of the distance from one end to the other of the chain of random steps, which was the intensity of the light, is the sum of the intensities of the separate pieces. And so, by the same kind of mathematics, we can prove immediately that if RN is the vector distance from the origin after N steps, the mean square of the distance from the origin is proportional to the number N of steps. That is, ⟨R2N⟩=NL2, where L is the length of each step. Since the number of steps is proportional to the time in our present problem, the mean square distance is proportional to the time:

This does not mean that the mean distance is proportional to the time. If the mean distance were proportional to the time, it would mean that the drifting is at a nice uniform velocity. The sailor is making some relatively sensible headway, but only such that his mean square distance is proportional to time. That is the characteristic of a random walk.
We may show very easily that in each successive step the square of the distance increases, on the average, by L2. For if we write RN=RN−1+L, we find that R2N is
RN⋅RN=R2N=R2N−1+2RN−1⋅L+L2,
and averaging over many trials, we have ⟨R2N⟩=⟨R2N−1⟩+L2, since ⟨RN−1⋅L⟩=0. Thus, by induction,

Now we would like to calculate the coefficient α in Eq. (41.17), and to do so we must add a feature. We are going to suppose that if we were to put a force on this particle (having nothing to do with the Brownian movement—we are taking a side issue for the moment), then it would react in the following way against the force. First, there would be inertia. Let m be the coefficient of inertia, the effective mass of the object (not necessarily the same as the real mass of the real particle, because the water has to move around the particle if we pull on it). Thus, if we talk about motion in one direction, there is a term like m(d2x/dt2) on one side. And next, we want also to assume that if we kept a steady pull on the object, there would be a drag on it from the fluid, proportional to its velocity. Besides the inertia of the fluid, there is a resistance to flow due to the viscosity and the complexity of the fluid. It is absolutely essential that there be some irreversible losses, something like resistance, in order that there be fluctuations. There is no way to produce the kT unless there are also losses. The source of the fluctuations is very closely related to these losses. What the mechanism of this drag is, we will discuss soon—we shall talk about forces that are proportional to the velocity and where they come from. But let us suppose for now that there is such a resistance. Then the formula for the motion under an external force, when we are pulling on it in a normal manner, is
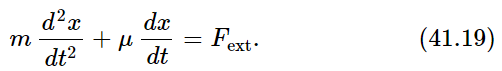
The quantity μ can be determined directly from experiment. For example, we can watch the drop fall under gravity. Then we know that the force is mg, and μ is mg divided by the speed of fall the drop ultimately acquires. Or we could put the drop in a centrifuge and see how fast it sediments. Or if it is charged, we can put an electric field on it. So μ is a measurable thing, not an artificial thing, and it is known for many types of colloidal particles, etc.
Now let us use the same formula in the case where the force is not external, but is equal to the irregular forces of the Brownian movement. We shall then try to determine the mean square distance that the object goes. Instead of taking the distances in three dimensions, let us take just one dimension, and find the mean of x2, just to prepare ourselves. (Obviously the mean of x2 is the same as the mean of y2 is the same as the mean of z2, and therefore the mean square of the distance is just 3 times what we are going to calculate.) The x-component of the irregular forces is, of course, just as irregular as any other component. What is the rate of change of x2? It is d(x2)/dt=2x(dx/dt), so what we have to find is the average of the position times the velocity. We shall show that this is a constant, and that therefore the mean square radius will increase proportionally to the time, and at what rate. Now if we multiply Eq. (41.19) by x, mx(d2x/dt2)+μx(dx/dt)=xFx. We want the time average of x(dx/dt), so let us take the average of the whole equation, and study the three terms. Now what about x times the force? If the particle happens to have gone a certain distance x, then, since the irregular force is completely irregular and does not know where the particle started from, the next impulse can be in any direction relative to x. If x is positive, there is no reason why the average force should also be in that direction. It is just as likely to be one way as the other. The bombardment forces are not driving it in a definite direction. So, the average value of x times F is zero. On the other hand, for the term mx(d2x/dt2) we will have to be a little fancy, and write this as
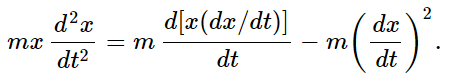
Thus, we put in these two terms and take the average of both. So let us see how much the first term should be. Now x times the velocity has a mean that does not change with time, because when it gets to some position it has no remembrance of where it was before, so things are no longer changing with time. So this quantity, on the average, is zero. We have left the quantity mv2, and that is the only thing we know: mv2/2 has a mean value 1/2 kT. Therefore, we find that
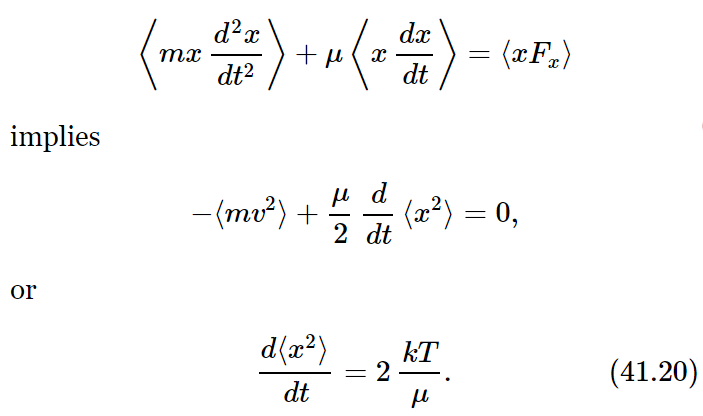
Therefore, the object has a mean square distance ⟨R2⟩, at the end of a certain amount of t, equal to

And so we can actually determine how far the particles go! We first must determine how they react to a steady force, how fast they drift under a known force (to find μ), and then we can determine how far they go in their random motions. This equation was of considerable importance historically, because it was one of the first ways by which the constant k was determined. After all, we can measure μ, the time, how far the particles go, and we can take an average. The reason that the determination of k was important is that in the law PV=RT for a mole, we know that R, which can also be measured, is equal to the number of atoms in a mole times k. A mole was originally defined as so and so many grams of oxygen-16 (now carbon is used), so the number of atoms in a mole was not known, originally. It is, of course, a very interesting and important problem. How big are atoms? How many are there? So, one of the earliest determinations of the number of atoms was by the determination of how far a dirty little particle would move if we watched it patiently under a microscope for a certain length of time. And thus, Boltzmann’s constant k and the Avogadro number N0 were determined because R had already been measured.
 الاكثر قراءة في فيزياء الجسيمات
الاكثر قراءة في فيزياء الجسيمات
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















