المجال الكهربائي

لقد وجد انه من المناسب مناقشة القوة الكهربائية بدلالة مفهوم يطلق عليه المجال الكهربائي. ويفي هذا المفهوم في الكهربائية بنفس الغرض الذي يفي به مفهوم مجال الجاذبية في الميكانيكا. وقبل ان نبدأ في مناقشة هذا المفهوم الجديد بالتفصيل سنقوم بمراجعة الموقف الأكثر شيوعاً لمجال الجاذبية.

لقد اعتدنا على حقيقة ان الكرة الارضية تؤثر بقوة الجاذبية المتجهة نحو مركزها على الأجسام الموجود على السطح او فوقه. ويؤثر القمر والكواكب الأخرى بقوى مماثلة على الأجسام القريبة منها. ولكي نصف هذه التأثيرات فإننا نقول ان هناك مجالاً للجاذبية في هذه المناطق. وعند أية نقطة فغن المجال يعتبر في اتجاه القوة التي بتأثير بها الجسم هناك. وتكون شدة المجال متناسبة مع شدة تلك القوة.

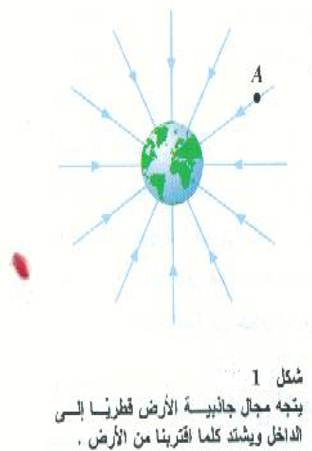
ومن المناسب أن نخطط مجالات الجاذبية؛ وبالنسبة للكرة الأرضية فإن مجال الجاذبية يبدو كما هو موضح بالشكل ((1 الذ يمكن تفسيره على النحو التالي:

لو أن جسماً وضع عند النقطة A ، فإنه سيتأثر بقوة في اتجاه رأس السهم نحو مركز الأرض. أما الخطوط وتسمى خطوط المجال فإنه تشير إلى اتجاه جذب الأرض؛ وهو ما يعتبر اتجاه مجال الجاذبية ( وفي الحقيقة فإن الشكل (1) لابد وأن يرسم في أبعاد ثلاثة. بحيث تتجه خطوط القوة دائماً ومن جميع الاتجاهات نحو مركز الأرض ).

وخطوط المجال لا تمثل اتجاه القوة فحسب ولكنها تعتبر مؤشراً على المقدار النسبي لها. ويمكنك ملاحظة ذلك في الشكل ((1 حيث تكون الخطوط اكثر تقارباً من بعضها البعض بالقرب من الأرض، حيث تكون القوة كبيرة، وذلك بالمقارنة مع الوضع بعيداً عن الأرض حيث تكون القوة أضعف. وسوف نعود إلى هذه السمة لخطوط المجال بعد أن نناقش المجال الكهربي، الذي يصف القوى الكهربية التي تؤثر بها الأجسام المشحونة على بعضها البعض ويمثل المجال الكهربي القوة الكهربية التي تتأثر بها شحنة موجبة ساكنة. ولننظر كيف يمكنك المضي قدماً نحو تعيين المجال الكهربي في منطقة ما. فيمكنك ببساطة وضع جسم مشحون (وسنطلق عليه شحنة اختبار) في المنطقة المذكورة. ثم تقوم بحساب القوة المؤثرة عليه من جابن الشحنات الأخرى كلها. على ان شحنة الاختبار تؤثر هي الأخرى بقوى على كل الشحنات الأخرى الموجودة بجوارها.

ولو ان هذه الشحنات كانت داخل فلز ( معدن) فإنها ستبدأ في التحرك. ولتغلب على هذه الصعوبة فسنتخيل أن شحنة الاختيار تتمتع بخاصية فريدة وهي ان: شحنة الاختبار ما هي إلا شحنة وهمية لا تؤثر بأي قوى على الشحنات القريبة منها. وسنقوم بالرمز لها بالحرف q₁ ويمكننا ــ من الناحية العملية ــ تقريب مفهوم شحنة الاختبار باستخدام شحنة ضئيلة للغاية لا تؤثر على الشحنات المجاورة إلا بقدر مهمل تماماً.

سنعتبر اتجاه المجال الكهربي في نفطة ما على أنه نفس اتجاه القوة المؤثرة على شحنة اختيار موجبة موضوعة في تلك النقطة. ولنفترض مثلاً ان شحنة اختبار موجبة قد وضعت عند النقطة A في الشكل (2 أ). إنها تنجذب قطرياً إلى الداخل، كما يوضح السهم المرسوم عند A وبالفعل، فإن القوة المؤثرة على شحنة الاختبار الموجبة ستتجه قطرياً إلى الداخل بغض النظر عن الموقع الذي تشغله بجوار الشحنة السالبة الموجودة بالمركز. وعلى هذا فإننا سنخمن أن المجال الكهربي يتجه كما هو موضع بالأسهم: يتجه المجال الكهربي بالقرب من شجنة سالبة نحو الشحنة نفسها.

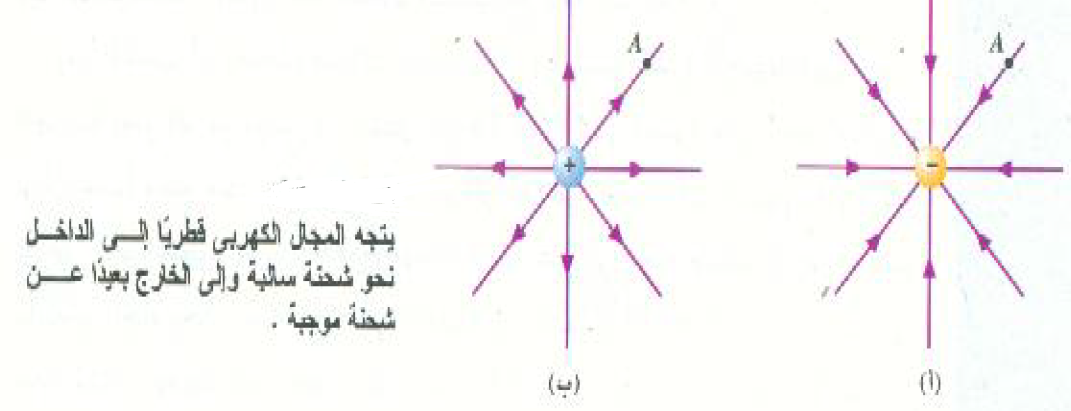
الشكل ((2

ويمكننا أيضاً تعيين اتجاه المجال بالقرب من شحنة موجبة بنفس الأسلوب، كما هو موضح في الشكل (2 ب). وشحنة الاختبار الموجبة تدفع قطرياً إلى الخارج بتأثير الشحنة الموجبة الموجودة بالمركز. ولذلك يتجه المجال الكهربي بالقرب من شحنة موجبة قطرياً بعيداً عن الشحنة.

والخطوط الموجهة التي رسمناها في الشكل (2) لبيان اتجاه الكهربي، تسمى خطوط المجال الكهربي. وكما رأينا فإن خطوط المجال الكهربي تنبع وتتجه بعيداً عن الشحنات الموجية، وتصب وتتجه نحو الشحنات السالبة.

ولكي يكتسب مفهوم المجال الكهربي معنى كمياً، فإننا سنعرف كمية تسمى شدة المجال الكهربي E. ويكون اتجاه E عند أية نفطة معينة باعتباره كمية متجهة هو نفس اتجاه خطوط المجال الكهربي المارة خلال تلك النقطة. اما مقدار E فهو يساوي القوة التي تتأثر بها شحنة الاختبار مقسومة على مقدار تلك الشحنة q₁:

(1)         E = F/q₁

وهكذا فإن وحدات E ستعرف على أنها N/C. وحيث ان E هي قوة لوحدة الشحنات، فإننا دائماً ما ننص على أنها قوة لوحدة شحنات الاختبار الموجبة. على ان علينا إدراك انه عند قياس شدة مجال كهربي قد نستخدم شحنة أصغر بكثير من 1 C حتى لا نثير أي اضطراب للشحنات الأخرى الموجودة بجوارها.

مواضيع ذات صلة

Thermal conductivity

Molecular diffusion

Ionic conductivity

The drift speed

Electrical transients

الشرر المقدس

الحقول الكهربية والشرر

الخلق غير المرئي

عجائب الكهرباء

مصادر الطاقة الكهربائية

التيارات الكهربائية التي تجري إلى الابد

النقل الكهربائي وقانون أوم