
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Using Quantum Mechanics
المؤلف:
Roger J Blin-Stoyle, FRS
المصدر:
Physics of Particles, Matter and the Universe
الجزء والصفحة:
P 76
22-5-2016
2572
Using Quantum Mechanics
The foregoing discussion has underlined the importance of using the wavelike properties of particles to understand certain physical phenomena. Clearly this approach had to be encompassed more formally in a theory which would enable the form and implications of these waves to be dealt with mathematically in just the same way that classical theory was encompassed in Newton’s Laws of Motion and electromagnetic theory. As mentioned earlier, the key physicists responsible for this development were Heisenberg and Schrodinger. The latter developed an equation the Schrodinger Equation which enabled the wavelike nature of a physical system to be described mathematically by a quantity called the wave function of the system. Associated physical quantities such as energy could also be deduced from the equation. A key element was that the wave function should make

Figure 1.1: (a) Wave functions and energies for a particle in an infinite potential well. (b) Oscillator energies.
physical sense. For example it should only have one value at any point, otherwise an unacceptable ambiguity would be introduced into physics; if it had two values it would be unclear which one should be used to determine the probability of finding the associated particle at that point. This means that the wave function has to be continuous; it cannot jump from one value to another at the same point. It is requirements of this sort that lead to the quantization of energies in a system first envisaged for an oscillator by Planck. The way in which this can happen can be illustrated most simply for a particle confined in a potential well with infinite sides. Wells were discussed. An infinite well is rather artificial but is much easier to deal with. Classically the particle in such a well can, in principle, have any energy from zero upwards; this is not the case with quantum mechanics. Since the particle is confined to the well (it has infinite sides), and cannot possibly escape, the wave function outside must be zero there is zero probability of finding the particle there. This means that, if the wave function is continuous, the part inside the well must be zero at the two edges so as to join, without jumping, the zero wave function outside. A few different possibilities of arranging this are shown in figure 1.1(a) and it will be recognized that this is completely equivalent in mathematical terms to the different standing waves that can be set up on a vibrating string fixed at both ends. The longest wavelength (corresponding to the lowest momentum and energy) possible is for the lowest wave function in the diagram. But this lowest energy is not zero: zero energy would require zero momentum and, therefore, infinite wavelength. This means that quantum mechanics does not allow a particle to sit at the bottom of the well with no energy at all. This minimum energy that a confined particle must have is referred to as zero point energy. A few possible standing waves having increasingly shorter wavelengths and corresponding to higher allowed energies are shown in the diagram. We have here an example of quantized energies-only specific values are allowed. These are referred to as energy levels and are analogous to the different harmonics for a vibrating string. Roughly speaking, the more ‘wiggly’ a wave function the higher the associated energy. Consider now the more complicated (mathematically) situation of a particle which classically can oscillate with frequency v. The potential well is identical in shape with that for a pendulum bob and is reproduced in figure 1.1(b). Again the requirement that the wave function should be ‘well behaved’ limits the allowed energies, the lowest ones being shown in the diagram. It will be noted that the energy levels are separated by hv as suggested by Planck and are given by the simple formula
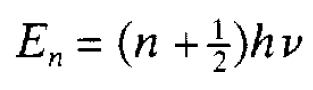
where n can take the values 0,1,2. . .. The quantity n is known as a quantum number and such numbers occur in all quantum formulations giving the allowed energies of a system. It will be noted here that the lowest energy of an oscillator is hv/2 and not zero as hypothesized by Planck. This energy, like the zero-point energy for the infinite potential well, reflects the uncertainty relation. If the particle were at the bottom of the oscillator potential well with zero energy (i.e. zero momentum) there would be no uncertainty in its position or its momentum, contrary to the relation. The shape of the wave functions corresponding to the different oscillator energy levels are also shown in figure 1.1(b) and it can be seen that they extend beyond the potential energy curve. This means that there is a finite probability of the particle being in a region which is not allowed classically. This has the implication that particles can penetrate barriers and can escape from situations where, classically, they would be confined. Consider, for example, a particle confined by two potential barriers (a sort of one dimensional box) as shown in figure 1.2. The particle energy is lower than the height of the barrier and so classically it cannot escape. However, as the diagam indicates, penetration of the wave function through the potential barrier takes place and this means that there is a finite probability of finding the particle outside the box. This, of course, is a quantum effect and is so small that it has no bearing on the use of boxes in everyday life. However it is of importance at the atomic and nuclear level, for example in understanding aspects of alpha radioactivity in which alpha particles escape from the nucleus.

Figure 1.2: A particle in a one-dimensional box.
 الاكثر قراءة في ميكانيكا الكم
الاكثر قراءة في ميكانيكا الكم
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام) قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)


















