
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
الرنين في موجات دي برولي: الحالات المستقرة
المؤلف:
فريدريك بوش ، دافيد جيرد
المصدر:
اساسيات الفيزياء
الجزء والصفحة:
ص 1019
11-7-2016
2129
الرنين في موجات دي برولي: الحالات المستقرة
ان الموجات الميكانيكية مثل تلك التي تحدث في الأوتار والموجات الصوتية داخل الأنابيب، فقد اكتشفنا الأهمية الكبيرة لرنين الموجات، وتظل الأهمية قائمة أيضاً بالنسبة لموجات دي برولي. وسنقوم الآن بمعالجة موقف بسيط يتضمن حدوث رنين لموجات دي برولي.
القضية الأولى: جسيم داخل انبوبة
اعتبر أن لديك جسيماً كتلته m داخل أنبوبة ضيقة طولها L وطرفاها مغلقان كما هو واضح من الشكل (1 أ). وإذا كان هذا الجسيم سيتصرف كموجة فلابد أن موجية دي برولي المصاحبة له ستحدث رنيناً في الأنبوبة، كما يتضح من الأجزاء السفلية من الشكل، ويطلق على مثل هذا الرنين حالة مستقرة. وحيث أن الجسيم لا يستطيع مغادرة الأنبوبة، فلابد أن طرفيها يمثلان عقدتين. (تذكر أن سعات موجات دي برولي هي التي تدلنا على أكثر الاماكن احتمالاً لأن يوجد فيه الجسيم). وهكذا سيحدث الجسيم رنيناً داخل الانبوبة عندما يكون لموجة دي برولي المصاحبة للجسيم الأطوال الموجية التالية (تذكر أن المسافة بين عقدتين هو λ 1/3):
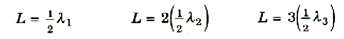
او بشكل عام، فأن الحالة المستقرة لجسيم ما ستحدث عندما:
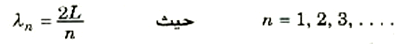
ولن يحدث الجسيم رنيناً داخل الانبوبة إلا إذا كان له أحد هذه الأطوال الموجية الرنينية. قياساً على صور أخرى درسناها للرنين نستطيع أن نستنبط ما يلي: لا تتنامى موجة كبيرة جداً داخل الانبوبة إلا عند رنين موجة فقط، فيما عدا ذلك تكون سعة الموجة صغيرة جداً لدرجة يمكن معها إهمالها. وحيث أن سعة موجة دي برولي بمثابة مقياس لاحتمال وجود الجسيم في مكان ما، فإننا نتوقع أن يتواجد الجسيم في الأنبوبة عند حدوث الرنين فقط. أضف إلى ذلك أن الجسيم سيتواجد بأكبر قدر من الاحتمالات حيث يكون لموجات الرنين المبينة في الشكل 1)) أقصى سعة، أي عند بطون الموجات. . أما حيث توجد العقد ــ وهذا الأمر أكثر إبهاراً ــ فإن الجسيم لن يتواجد مطلقاً. وقبل أن نسترسل في فحص هذه النتيجة لأبعد من هذا، سنقوم بفحص طاقة الجسيم داخل الانبوبة.
ليس للجسيم سوى طاقة حركة ، mv2½ (نعتبر الآن ظروفاً غير نسبوية). وسنطلق على طاقة الجسيم En عندما يكون الجسيم في الحالة الرنينية التي رقمها n أي،
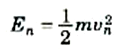
إلا أن كمية التحرك p هي mv ولذلك يمكننا كتابة التعبير السابق هكذا؛
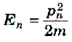
ولكن الطول الموجي لدى برولي المصاحب للجسيم هو n = h/pnλ ولذلك،

وفي النهاية ، قد رأينا أن n = 2L/nλ، ومن ثم
(1) 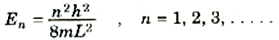
وهكذا نصل إلى النتيجة المدهشة وهي أنه لو كان على الجسيم أن يتواجد داخل الانبوبة فلابد أن يكون له إحدى قيم الطاقة المعطاة بالمعادلة (1) وعندئذ يقال أن طاقة الجسيم مكماة quantized ولهذا السبب يشار إلى الميكانيكا الموجية عادة باسم ميكانيكا الكم. ولن يكون للجسيم أي قيم للطاقة خلاف هذه القيم. وتتناقض هذه النتيجة المبهرة مع الميكانيكا الكلاسيكية، التي تتنبأ بأن الجسم داخل الأنبوبة قادر على اتخاذ أي وكل قيم طاقة الحركة بما فيها الصفر. ألا يجعلنا هذا التناقض بين نتائج الميكانيكا الموجية وخبراتنا المعروفة نكفر بالميكانيكا الموجية؟ الإجابة هي "لا" وذلك لسبب سنشرحه الآن.
دعنا نقم بحساب طاقات الرنين لحبيبة غبار دقيقة (m = 1×10-15 kg) داخل أنبوبة طولها 50 cm:
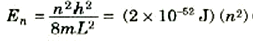
أي أن طاقات الحبيبة هي 2×10-52 J و4(2×10-52) و9(2×10-52) وهلم جراً. يلاحظ مدى ضآلة هذه الطاقات والفرق فيها بينهما. إن الفجوة بين قيمتين هي 2×10-52 J فحسب، وهي من الصغر بالمقارنة مع الطاقة الحرارية لجسم غازي (10-21) لدرجة أننا لن نستطيع معها أن نحكم إن كانت هناك فجوة للطاقة أم لا. بل إن هذا الأمر أكثر وضوحاً بالنسبة لجسيم ذي كتلة أكبر. ونستنتج من ثم أنه بالنسبة لجميع الجسيمات العادية داخل أنابيب ذات حجم مرئي، فإن طاقة الجسيم تكون متصلة بالضرورة؛ فالتجربة المعملية لا تسمح لنا برؤية الطبيعة الكمية للطاقة كما تتنبأ بها الميكانيكا الموجية.
ويصير الموقف مختلف تماماً عند معالجة أنابيب ذات أحجام ذرية. افترض أن لدينا إلكتروناً (m = 9×10-31 kg) داخل أنبوبة لا يزيد طولها عن 2×10-10 m، وإذن
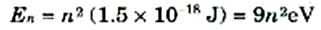
وهذه الطاقة من الكبر بحيث يصبح من السهل قياس فجوات الطاقة. ونستنتج من ثم، أن الطبيعة الموجية للجسيمات والسمة الكبيرة لطاقتها تكون ذات شان في النظم ذات الأحجام الذرية.
القضية الثانية: المتذبذب التوافقي
يطلق على كتلة m تهتز تحت تأثير قوة زنبرك تتبع قانون هوك متذبذباً توافقياً ويمكننا ــ كتقريب أولي ــ أن نعتبر الذرات المهتزة في الجزيئات، متذبذبات توافقية. ويتشابه المتذبذب التوافقي في كثير من الوجوه مع الجسيم داخل الأنبوبة الذي عالجنا منذ قليل، ولكن ما يعقد المشكلة هو حقيقة أن للنظام طاقة وضع متغيرة نتيجة تشوه الزنبرك. وحتى مع هذا فإن حركة النظام الرنينية يمكن إيجادها عند حل معادلة شرودنجر ــ والنتيجة النهائية لذلك الحساب ليست بالبعيدة تماماً عن تلك التي لجسيم داخل أنبوبة . وستكون الطاقة مكماة ــ بشكل خاص ــ ولها القيم التالية:

حيث k هو ثابت الزنبرك.
ويمكن التعبير عن هذه النتيجة بصورة مثيرة للاهتمام إذا تذكرنا أن تردد الرنين ... بالنسبة لكتلة معلقة عند نهاية زنبرك هو

وبالتعويض من هذه القيمة في معادلة En نجد ،
(2) 
أي أن طاقات متذبذب يخضع لقانون هوك مكماة، والفجوات بين الطاقات المسموح بها مساوية للمقدار 0hf.
هذه النتيجة العجيبة هي ببساطة الخاصية التي كان على بلانك أن يلصقها بالمتذبذبات حتى يتمكن من تفسير إشعاع الجسم الأسود. أي أنه بعد مرور 25 سنة على ما خمنه بلانك، يأتي استخدام مفاهيم دي برولي الموجية ويبين السبب في أن التخمين لابد أن يكون صحيحاً. أن فرض بلانك لا يمكن اختياره بالنسبة لمتذبذبات ذات حجم معملي. ونرى الآن أن هذا التخمين غير القائم على دليل، قد تمت مؤازرته بالعديد من صور نجاح النظرية الكمية.