الانكسار عند الأسطح الكروية

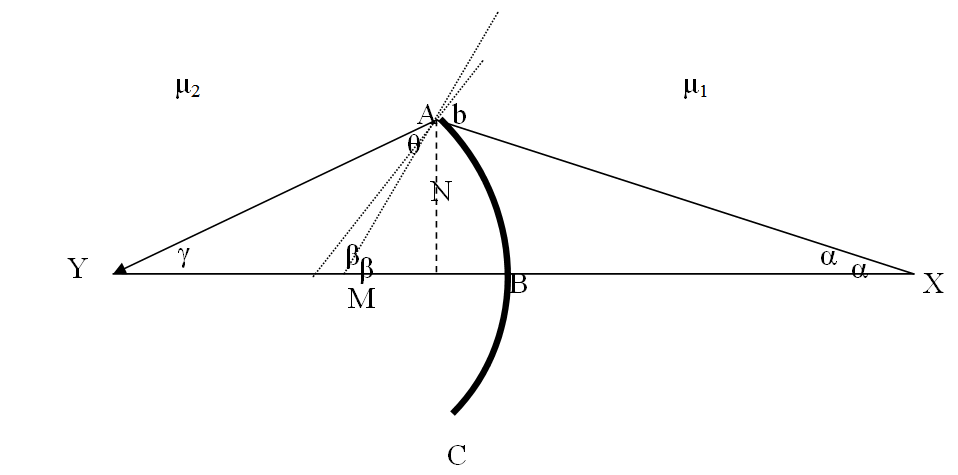
نفرض أن X نقطة مضيئة على المحور الأساسي لمرآة مقعرة ABC تفصل بين وسطين معامل انكسار الضوء فيهما μ₁ و μ₂ و ليكنM  مركز تكور السطح الكروي.

فإذا فرضنا أن μ₁ <  μ₂  فان الشعاع الساقط  XA  ينكسر في الاتجاه AY^/  ، و إذا مددنا هذا الشعاع المنكسر فانه سوف يتقاطع مع محور المرآة في النقطة Y التي تمثل صورة الجسم، كما هو موضح بالشكل الاتي.

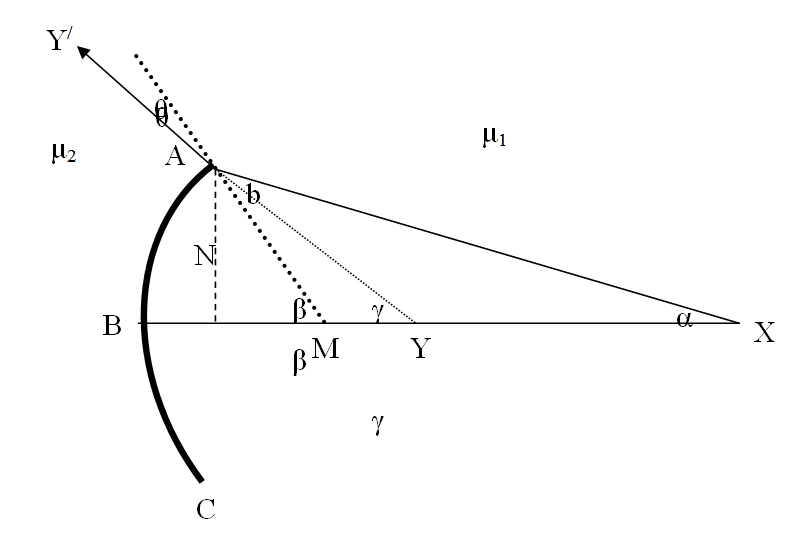
و من هذا الشكل يتضح أن

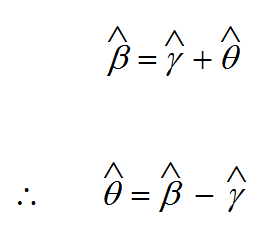 (1)

أيضا

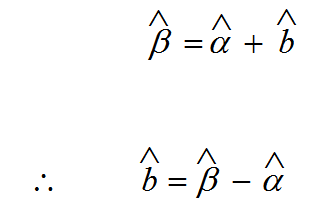 (2)

و حيث أن

فإذا كانت النقطة  A  قريبة  من قطب المرآة فأن كل من زاويتي السقوط و الانكسار تكونان صغيرتين

 (3)

بالتعويض من  (1)   و  (2)   في   (3)  نحصل على

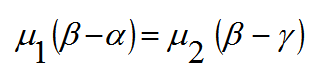 (4)

فإذا كانت المسافة بين الجسم و الصورة و المركز عن قطب المرآة هي  r, y, x على الترتيب، فان

  (*)

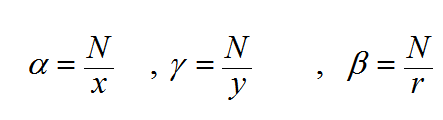بالتعويض من هذه المعادلة في المعادلة (4)

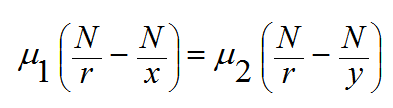
و وفقا لقاعدة الإشارات التي سبق ذكرها فان:

    (5)

و هي المعادلة العامة في حالة السطح الكرى المقعر.

أما في حالة السطح الكرى المحدب (كما بالشكل الآتي) فان

 (6)

أيضا

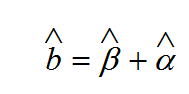  (7)

و من المعادلات (3)  و (6)  و (7)   يمكننا الحصول على

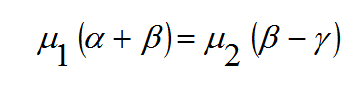 (8)

و بكتابة المعادلة  (*)  مرة أخر و لكن مع مراعاة قاعدة الإشارات في هذه الحالة

فان المعادلة (51)  تأخذ الشكل الآتي

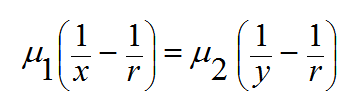 (9)

 (10)

و هي نفس النتيجة التي حصلنا عليها في حالة السطح الكرى المقعر.

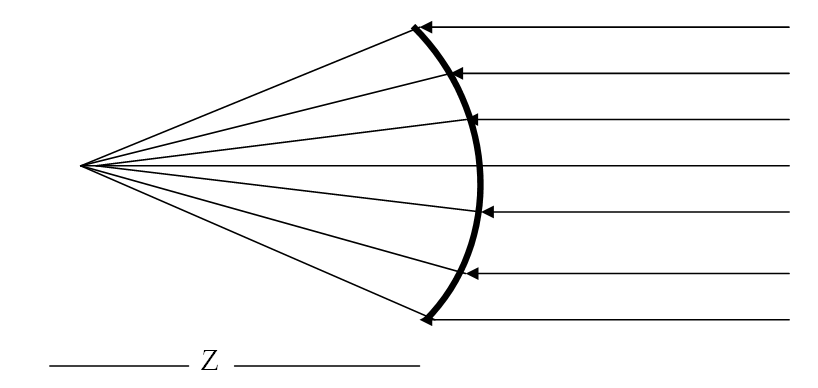
أما إذا كانت الأشعة الساقطة متوازية كما بالشكل الآتي ( أي أن X في ∞) فان المعادلة السابقة تصبح على الصورة الآتية

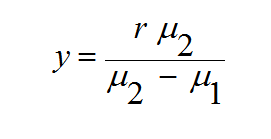 (11)

و بذلك تتجمع الأشعة المنكسرة في نقطة واحدة Z  تسمى البؤرة  و يسمى بعدها عن قطب المرآة البعد البؤري.

مواضيع ذات صلة

The momentum of light

Polarization of scattered light

The electric vector of light

Scattering of light

Reflection and refraction

Light

لم يرتدي البحارة نظارات شمسية؟

أسرار قوس قزح

المفعول الكهروضوئي والنظرية الجسيمية والموجية:

الاضطراب في تفسير بنية الضوء (الطبيعة الجسمية الموجية للضوء)

الضوء

الضوء ومم يتالف