Triple Pendulum
المؤلف:
Sidney B. Cahn Boris E. Nadgorny
المصدر:
A GUIDE TO PHYSICS PROBLEMS
الجزء والصفحة:
part 1 , p 21
2-8-2016
2716
Triple Pendulum
A triple pendulum consists of masses αm, m, and m attached to a single light string at distances a, 2a and 3a respectively from its point of suspension (see Figure 1.1).
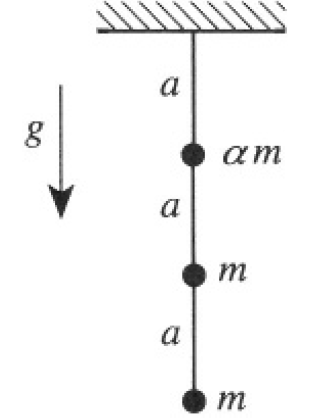
Figure 1.1
a) Determine the value of α such that one of the normal frequencies of this system will equal the frequency of a simple pendulum of length a/2 and mass m. You may assume the displacements of the masses from equilibrium are small.
b) Find the mode corresponding to this frequency and sketch it.
SOLUTION
a) Write the Lagrangian of the system using coordinates φ1, φ2, φ3 (see Figure 1.2a).
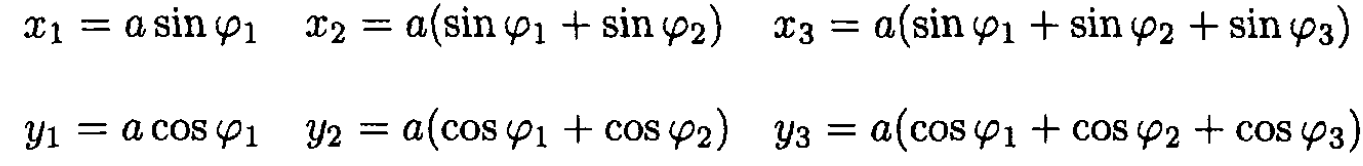
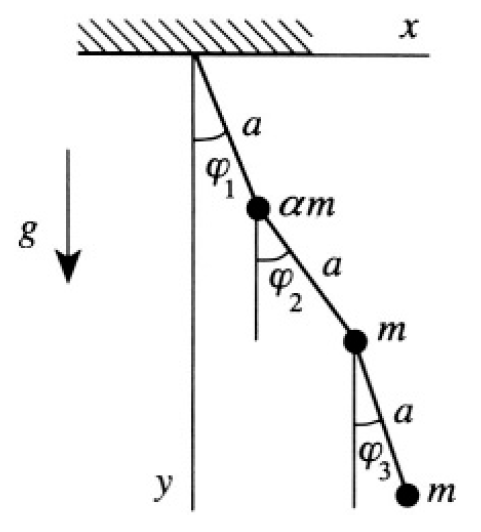
Figure 1.2a
Then in the small angle approximation,
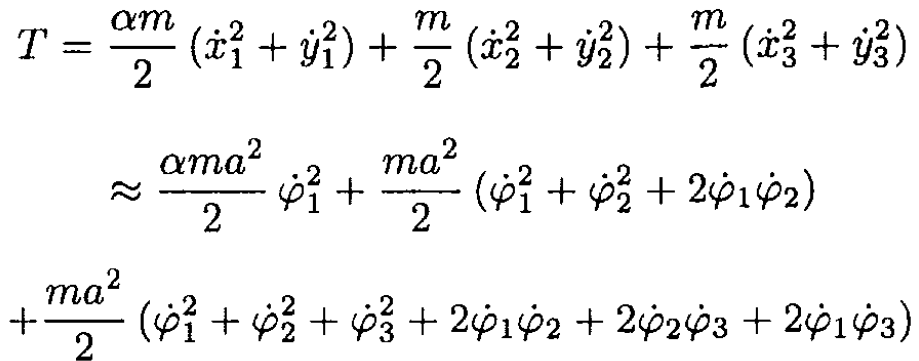
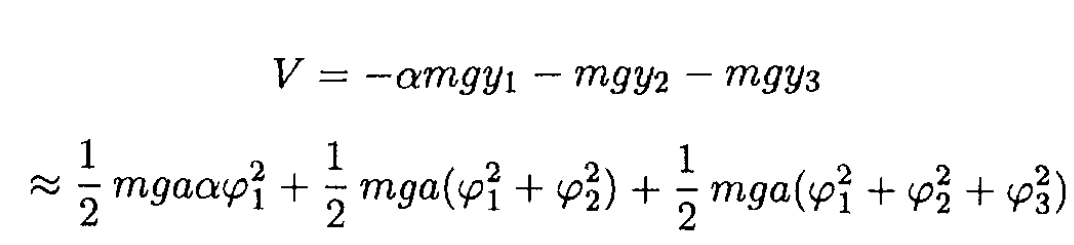
Here we used
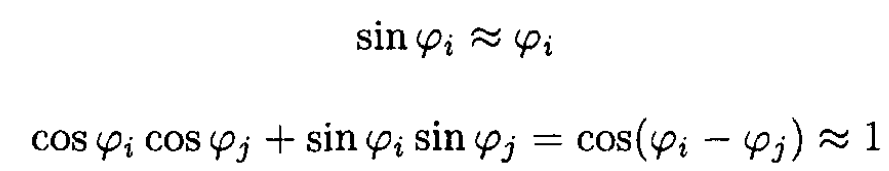
So the Lagrangian is
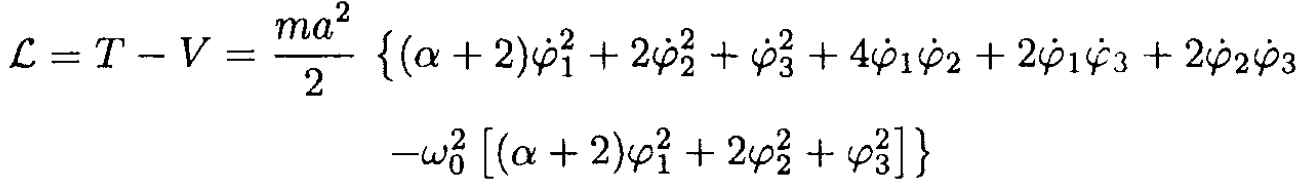
where we let g/a = ω20 Therefore the equations of motion will be
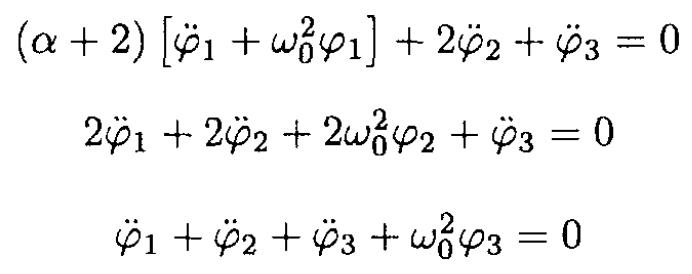
Looking for the solution in the form φi = Ai eiωt and letting ω2/ω20 = λ, we have as a condition for the existence of a nontrivial solution
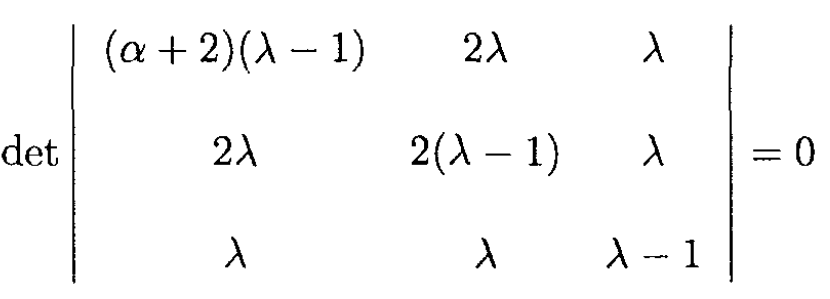
We want a mode where ω2 = 2g/a. So λ = 2, and the determinant becomes
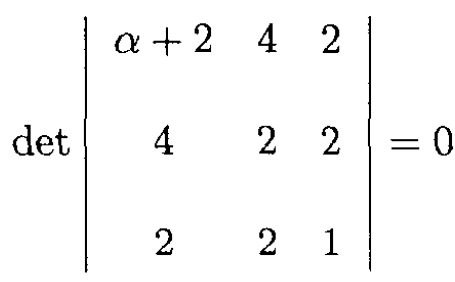
Obviously α = 2 is the only solution of this equation (the first and third rows are then proportional).
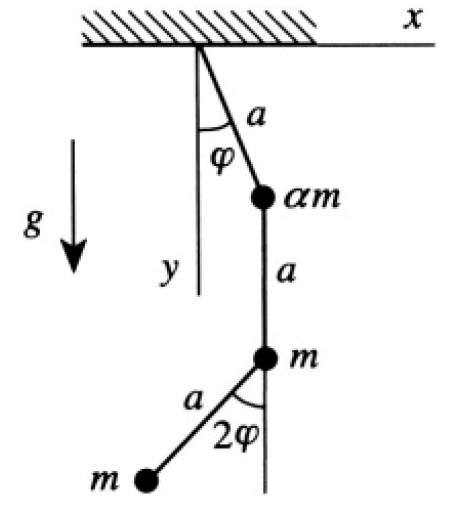
b) The mode corresponding to this frequency can be found from the equation
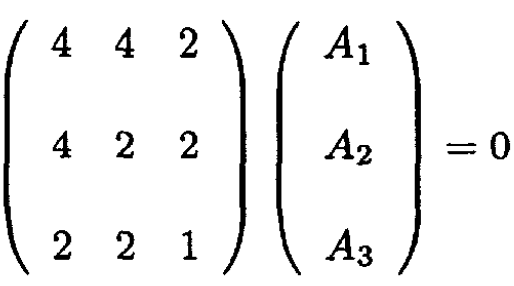
which has a solution A3 = -2A1, A2 = 0. So the mode corresponding to the frequency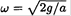 
is shown in Figure 1.2b
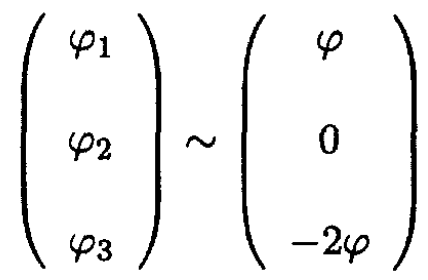
الاكثر قراءة في مواضيع اخرى
اخر الاخبار
اخبار العتبة العباسية المقدسة
