Ideal Gas in One-Dimensional Potential
المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
المصدر:
A GUIDE TO PHYSICS PROBLEMS
الجزء والصفحة:
part 2 , p 21
30-8-2016
1464
Ideal Gas in One-Dimensional Potential
a) An ideal gas of particles, each of mass m, at temperature τ, is subjected to an external force whose potential energy has the form
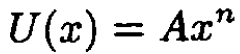
with 0 ≤ x ≤ ∞, A > 0, and n > 0. Find the average potential energy per particle.
b) What is the average potential energy per particle in a gas in a uniform gravitational field?
SOLUTION
a) The coordinate- and momentum-dependent parts of the partition function can be separated. The coordinate-dependent part of the partition function
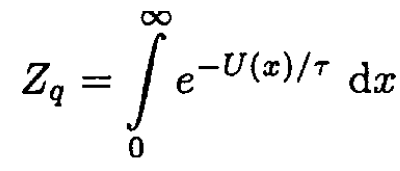(1)
For the potential in this case we have
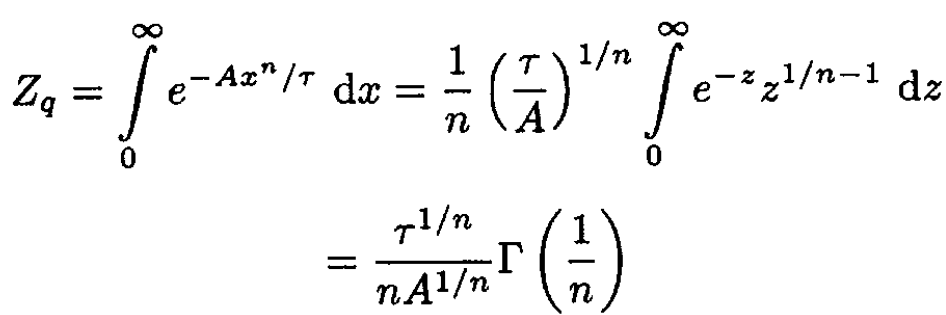(2)
where we substituted
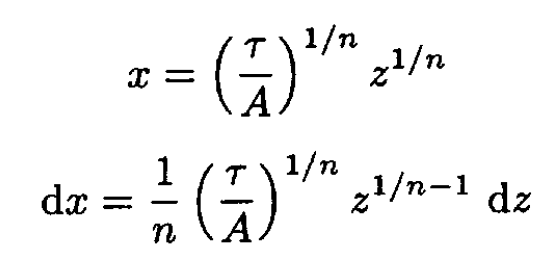
and
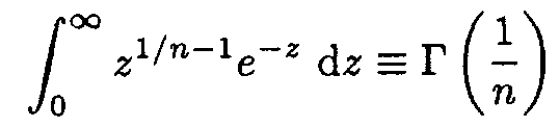
The free energy associated with the coordinate-dependent part of the partition function is
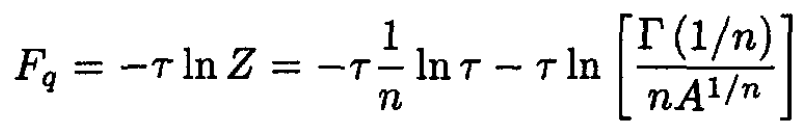(3)
The average potential energy is given by
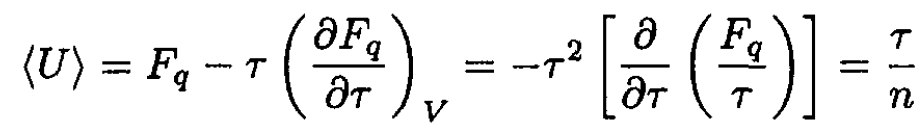(4)
For n = 2 we have a harmonic oscillator, and in agreement with the equipartition theorem
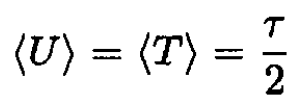
b) For n = 1, U = mgx, and the average potential energy per particle
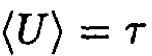
which also agrees with the generalized equipartition theorem.
الاكثر قراءة في مواضيع اخرى
اخر الاخبار
اخبار العتبة العباسية المقدسة
