We return once again to our usual setting:

for τ = τ [α(.)], the first time that x(τ ) = x¹. This is the fixed endpoint problem.

STATE CONSTRAINTS. We introduce a new complication by asking that our dynamics x(.) must always remain within a given region R ⊂ Rⁿ. We will as above suppose that R has the explicit representation

                                  R = {x ∈ Rⁿ | g(x) ≤ 0}

for a given function g(.) : Rⁿ → R.

DEFINITION. It will be convenient to introduce the quantity

                          c(x, a) := ∇g(x) .f (x, a).

Notice that

if x(t) ∈ ∂R for times s₀ ≤ t ≤ s₁, then c(x(t),α(t)) ≡ 0 (s₀ ≤ t ≤ s₁).

This is so since f is then tangent to ∂R, whereas ∇g is perpendicular.

Then there exists a costate function p^∗(.) : [s₀, s₁] → Rⁿ such that (ODE) holds.

There also exists λ^∗(.) : [s₀, s₁] → R such that for times s₀ ≤ t ≤ s₁ we have

To keep things simple, we have omitted some technical assumptions really needed for the Theorem to be valid.

REMARKS AND INTERPRETATIONS (i) Let A ⊂ R^m be of this form:

                           A = {a ∈ R^m | g₁(a) ≤ 0, . . . , g_s(a) ≤ 0}

for given functions g₁, . . . , g_s : R^m → R. In this case we can use Lagrange multipliersto deduce from (M′) that

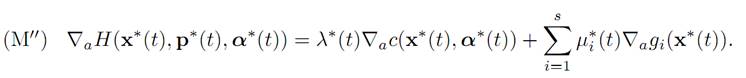
The function λ^∗(.) here is that appearing in (ADJ′).

If x^∗(t) lies in the interior of R for say the times 0 ≤ t < s₀, then the ordinary Maximum Principle holds.

(ii) Jump conditions. In the situation above, we always have

p^∗ (s₀ − 0) = p∗(s₀ + 0),  

where s₀ is a time that x^∗ hits ∂R. In other words, there is no jump in p^∗ when we hit the boundary of the constraint ∂R.

 However,

p^∗ (s₁ + 0) = p^∗ (s₁ − 0) − λ^∗ (s₁)∇g(x^∗ (s₁));

References

[B-CD] M. Bardi and I. Capuzzo-Dolcetta, Optimal Control and Viscosity Solutions of Hamilton-Jacobi-Bellman Equations, Birkhauser, 1997.

[B-J] N. Barron and R. Jensen, The Pontryagin maximum principle from dynamic programming and viscosity solutions to first-order partial differential equations, Transactions AMS 298 (1986), 635–641.

[C1] F. Clarke, Optimization and Nonsmooth Analysis, Wiley-Interscience, 1983.

[C2] F. Clarke, Methods of Dynamic and Nonsmooth Optimization, CBMS-NSF Regional Conference Series in Applied Mathematics, SIAM, 1989.

[Cr] B. D. Craven, Control and Optimization, Chapman & Hall, 1995.

[E] L. C. Evans, An Introduction to Stochastic Differential Equations, lecture notes avail-able at http://math.berkeley.edu/˜ evans/SDE.course.pdf.

[F-R] W. Fleming and R. Rishel, Deterministic and Stochastic Optimal Control, Springer, 1975.

[F-S] W. Fleming and M. Soner, Controlled Markov Processes and Viscosity Solutions, Springer, 1993.

[H] L. Hocking, Optimal Control: An Introduction to the Theory with Applications, OxfordUniversity Press, 1991.

[I] R. Isaacs, Differential Games: A mathematical theory with applications to warfare and pursuit, control and optimization, Wiley, 1965 (reprinted by Dover in 1999).

[K] G. Knowles, An Introduction to Applied Optimal Control, Academic Press, 1981.

[Kr] N. V. Krylov, Controlled Diffusion Processes, Springer, 1980.

[L-M] E. B. Lee and L. Markus, Foundations of Optimal Control Theory, Wiley, 1967.

[L] J. Lewin, Differential Games: Theory and methods for solving game problems with singular surfaces, Springer, 1994.

[M-S] J. Macki and A. Strauss, Introduction to Optimal Control Theory, Springer, 1982.

[O] B. K. Oksendal, Stochastic Differential Equations: An Introduction with Applications, 4th ed., Springer, 1995.

[O-W] G. Oster and E. O. Wilson, Caste and Ecology in Social Insects, Princeton UniversityPress.

[P-B-G-M] L. S. Pontryagin, V. G. Boltyanski, R. S. Gamkrelidze and E. F. Mishchenko, The Mathematical Theory of Optimal Processes, Interscience, 1962.

[T] William J. Terrell, Some fundamental control theory I: Controllability, observability,  and duality, American Math Monthly 106 (1999), 705–719.

مواضيع ذات صلة

DYNAMIC PROGRAMMING-DYNAMIC PROGRAMMING AND THE PONTRYAGIN MAXIMUM PRINCIPLE

DYNAMIC PROGRAMMING-EXAMPLES

DERIVATION OF BELLMAN,S PDE-DYNAMIC PROGRAMMING

THE PONTRYAGIN MAXIMUM PRINCIPLE-MORE APPLICATIONS

THE PONTRYAGIN MAXIMUM PRINCIPLE-MORE APPLICATIONS

THE PONTRYAGIN MAXIMUM PRINCIPLE-MAXIMUMPRINCIPLEWITH TRANSVERSALITY CONDITIONS

THE PONTRYAGIN MAXIMUM PRINCIPLE-APPLICATIONS AND EXAMPLES

THE PONTRYAGIN MAXIMUM PRINCIPLE-STATEMENT OF PONTRYAGIN MAXIMUM PRINCIPLE

THE PONTRYAGIN MAXIMUM PRINCIPLE-REVIEW OF LAGRANGE MULTIPLIERS.

THE PONTRYAGIN MAXIMUM PRINCIPLE-CALCULUS OF VARIATIONS, HAMILTONIAN DYNAMICS

LINEAR TIME-OPTIMAL CONTROL-EXAMPLES

LINEAR TIME-OPTIMAL CONTROL-THE MAXIMUM PRINCIPLE FOR LINEAR TIME-OPTIMAL CONTROL