
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Doppler Effect
المؤلف:
Professor John W. Norbury
المصدر:
ELEMENTARY MECHANICS & THERMODYNAMICS
الجزء والصفحة:
p 205
1-1-2017
2487
Doppler Effect
Everyone has noticed the pitch of the sound of a train varies when the train passes. You can also easily hear this just listening to cars drive down the road. This change in frequency of a moving sound source is called the Doppler effect. The same Doppler effect is also observed when the listener is moving and the source is stationary. We have previously seen that for a stationary observer and source, then
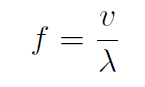
where v is the wave speed and ¸ is the wavelength.
Example An observer moves toward a stationary source of sound waves at a speed vD (detector speed). Derive a formula for the observed frequency f ʹ in terms of the stationary frequency f.
Solution The detector will sense a higher frequency as in
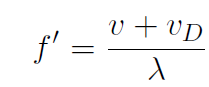
Now

or

Note: if the observer was moving away, the result would be
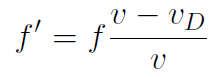
Example A sound wave moves toward a stationary observer at a speed vs. Derive a formula for the observed frequency f ʹ in terms of the stationary frequency f.
Solution This time it is the wavelength which changes and it will be smaller as in
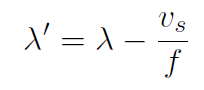
f ʹ is now (due to change in λʹ)
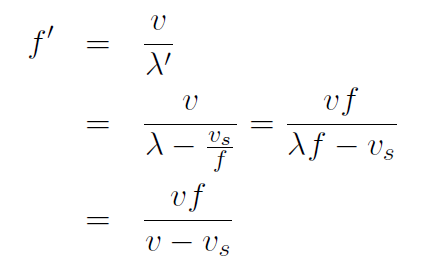
or

Note: if the source was smoving away, the result would be
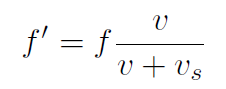
All of the previous results can be combined into a single formula,
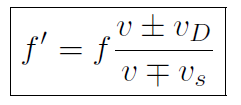
If vs = 0 we get  as before and if vD = 0 we get
as before and if vD = 0 we get  as before. An easy way to remember the signs is that if detector and source are moving toward each other the frequency increases. If they are moving away from each other the frequency decreases. The Austrian physicist, Johann Christian Doppler proposed the effect in 1842. In 1845 it was tested experimentally by Buys Ballot using a locomotive drawing an open train car with trumpeters playing.
as before. An easy way to remember the signs is that if detector and source are moving toward each other the frequency increases. If they are moving away from each other the frequency decreases. The Austrian physicist, Johann Christian Doppler proposed the effect in 1842. In 1845 it was tested experimentally by Buys Ballot using a locomotive drawing an open train car with trumpeters playing.
Example Middle C has a frequency of 264 Hz. The D note has a fequency of 300 Hz. If a trumpeter is playing the C note on a train, how fast would the train need to travel for a stationary person (with perfect pitch) on the ground to hear a D note ?
Solution Here vD = 0 and we want to find vs. The frequency increases and we have
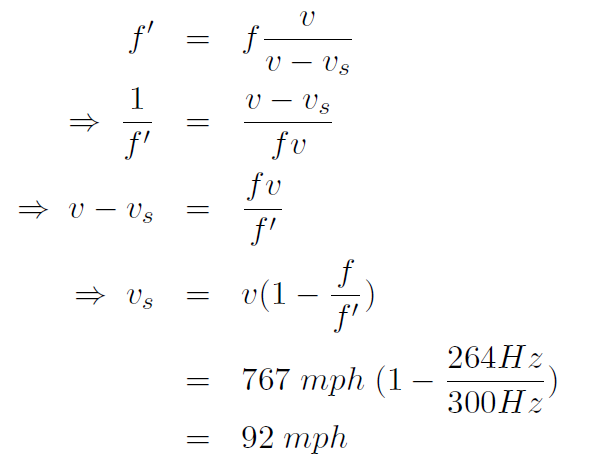
 الاكثر قراءة في الصوت
الاكثر قراءة في الصوت
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















