Acetic acid and other weak acids

Suppose that you dissolve acetic acid (CH₃COOH) in water. It reacts with the water molecules, donating a proton and forming hydronium ions. It also establishes equilibrium, where you have a significant amount of unionized acetic acid. The acetic acid reaction with water looks like this:

CH₃COOH(l) + H₂O(l) ↔ CH₃COO^– + H₃O⁺

The amount of hydronium ion that you get in solutions of acids that don’t ionize completely is much less than it is with a strong acid. Acids that only partially ionize are called weak acids. In the case of acetic acid, about 5 percent ionizes, and 95 percent remains in the molecular form.

Calculating the hydronium ion concentration in weak acid solutions isn’t as straightforward as it is in strong solutions, because not all the weak acid that dissolves initially has ionized. To calculate the hydronium ion concentration, you must use the equilibrium constant expression for the weak

acid.

For weak acid solutions, you use a modified equilibrium constant expression called the Ka — the acid ionization constant.  One way to distinguish between strong and weak acids is to look for an acid ionization constant (Ka) value. If the acid has a Ka value, then it’s weak. Take a look at the generalized ionization of some weak acid HA:

HA + H₂O ↔ A^– + H₃O⁺

The Ka expression for this weak acid is

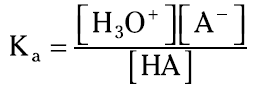
Note that the [HA] represents the molar concentration of HA at equilibrium, not initially. Also, note that the concentration of water doesn’t appear in the Ka expression, because there’s so much that it actually becomes a constant incorporated into the Ka expression.

Now go back to that acetic acid equilibrium. The Ka for acetic acid is 1.8 × 10^–5. The Ka expression for the acetic acid ionization is

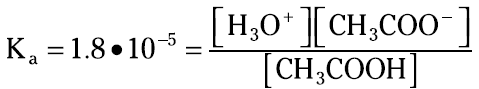
You can use this Ka when calculating the hydronium ion concentration in, say, a 2.0 M solution of acetic acid. You know that the initial concentration of acetic acid is 2.0 M. You know that a little bit has ionized, forming a little hydronium ion and acetate ion. You also can see from the balanced reaction that for every hydronium ion that’s formed, an acetate ion is also formed — so their concentrations are the same. You can represent the amount of [H₃O⁺] and [CH₃COO^–] as x, so

[H₃O⁺] = [CH₃COO^–] = x

To produce the x amount of hydronium and acetate ion, the same amount of ionizing acetic acid is required. So you can represent the amount of acetic acid remaining at equilibrium as the amount you started with, 2.0 M, minus the amount that ionizes, x:

[CH₃COOH] = 2.0 – x

For the vast majority of situations, you can say that x is very small in comparison to the initial concentration of the weak acid. So you can say that 2.0 – x is approximately equal to 2.0.

This means that you can often approximate the equilibrium concentration of the weak acid with its initial concentration. The equilibrium constant expression now looks like this:

مواضيع ذات صلة

التفاعل مع اصباغ الازو

تفاعل الجالكونات مع البروم

تفاعل الجالكونات مع الهكسانون الحلقي

تفاعل الجالكونات مع اليوريا ومعوضاته

تفاعل الجالكونات مع البيروكسيدات

تفاعل الجالكون مع الهيدرازين والفنيل هيدرازين

مركبات الجالكون Chalcone Compounds

تفاعل إضافة مايكل

الاضافة الالكتروفيلية الى مركبات الكاربونيل ألفا – بيتا غير المشبعة

تفاعلات تكاثف مركبات الكاربونيل

تحضير مركبات الكاربونيل ألفا – بيتا غيرالمشبعة

مركبات الكاربونيل ألفا – بيتا غير المشبعة