Conductors in electrostatic equilibrium

A good electrical conductor, such as copper, contains charges (electrons) that are free to move within the material. When there is no net motion of charges within the conductor, the conductor is in electrostatic equilibrium

Conductor in electrostatic equilibrium has the following properties:

1. Any excess charge on an isolated conductor must reside entirely on its surface. (Explain why?) The answer is when an excess charge is placed on a conductor, it will set-up electric field inside the conductor. These fields act on the charge carriers of the conductor (electrons) and cause them to move i.e. current flow inside the conductor. These currents redistribute the excess charge on the surface in such away that the internal electric fields reduced to become zero and the currents stop, and the electrostatic conditions restore.

2. The electric field is zero everywhere inside the conductor. (Explain why?) Same reason as above

In figure 1.1 it shows a conducting slab in an external electric field E. The charges induced on the surface of the slab produce an electric field, which opposes the external field, giving a resultant field of zero in the conductor.

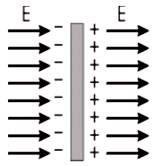
Figure 1.1

Steps which should be followed in solving problems:

1. The gaussian surface should be chosen to have the same symmetry as the charge distribution.

2. The dimensions of the surface must be such that the surface includes the point where the electric field is to be calculated.

3. From the symmetry of the charge distribution, determine the direction of the electric field and the surface area vector dA, over the region of the gaussian surface.

4. Write E. dA as E dA cosθ and divide the surface into separate regions if necessary.

5. The total charge enclosed by the gaussian surface is dq = ∫dq, which is represented in terms of the charge density (dq = λ dx for line of charge, dq = σdA for a surface of charge, dq = ρ dv for a volume of charge).

مواضيع ذات صلة

Thermal conductivity

Molecular diffusion

Ionic conductivity

The drift speed

Electrical transients

الشرر المقدس

الحقول الكهربية والشرر

الخلق غير المرئي

عجائب الكهرباء

مصادر الطاقة الكهربائية

التيارات الكهربائية التي تجري إلى الابد

النقل الكهربائي وقانون أوم