Electron Effective Mass

The movement of an electron in a lattice will, in general, be different from that of an electron in free space. In addition to an externally applied force, there are internal forces in the crystal due to positively charged ions or protons and negatively charged electrons, which will influence the motion of electrons in the lattice. We can write

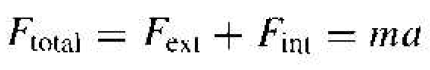(1)

where F_total, F_ext, and F_int, are the total force, the externally applied force, and the internal forces, respectively, acting on a particle in a crystal. The parameter a is the acceleration and m is the rest mass of the particle.

Since it is difficult to take into account all of the internal forces, we will write the equation

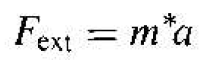(2)

where the acceleration a is now directly related to the external force. The parameter m*. called the effective mass, takes into account the panicle mass and also takes into account the effect of the internal forces.

To use an analogy for the effective mass concept, consider the difference in motion between a glass marble in a container filled with water and in a container filled

with oil. In general, the marble will drop through the water at a faster rate than through the oil. The external force in this example is the gravitational force and the internal forces are related to the viscosity of the liquids. Because of the difference in motion of the marble in these two cases, the mass of the marble would appear to be different in water than in oil. (As with any analogy, we must be careful not to be too literal.)

We can also relate the effective mass of an electron in a crystal to the E versus k curves. In a semiconductor material, we will be dealing with allowed energy hands that are almost empty of electrons and other energy bands that are almost full of electrons.

To begin, consider the case of a free electron whose E versus k curve. Recalling Equation (3.28). the energy and momentum are related by E = p²/2m = h²k²/2m, where m is the mass of the electron. The momentum an wave number k are related by p = hk. If we take the derivative of Equation (3.28) with respect to k, we obtain

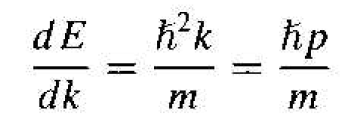(3)

Relating momentum to velocity, Equation (3) can be written as

(4)

where v is the velocity of the particle. The first derivative of E with respect to k is related to the velocity of the panicle.

If we now take the second derivative of E with respect to k, we have

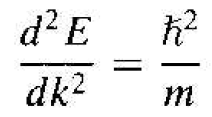(5)

We may rewrite Equation (5) as

(6)

The second derivative of E with respect to k is inversely proportional to the mass of the particle. For the case of a free electron, the mass is a constant (nonrelativistic effect), so the second derivative function is a constant. We may also that d²E/dk² is a positive quantity, which implies that the mass of the electron is also a positive quantity.

If we apply an electric field to the free electron and use Newton's classical equation of motion, we can write

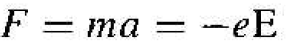(7)

where a is the acceleration, E is the applied electric field, and e ih the magnitude of the electronic charge. Solving for the acceleration, we have

(8)

The motion of the free electron is in the opposite direction to the applied electric field because of the negative charge.

We may now apply the results to the electron in the bottom of an allowed energy band. Consider the allowed energy band in Figure 1.1. The energy near the bottom of this energy band may be approximated by a parabola, just as that of a free particle. We may write

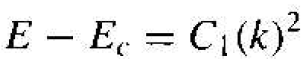(9)

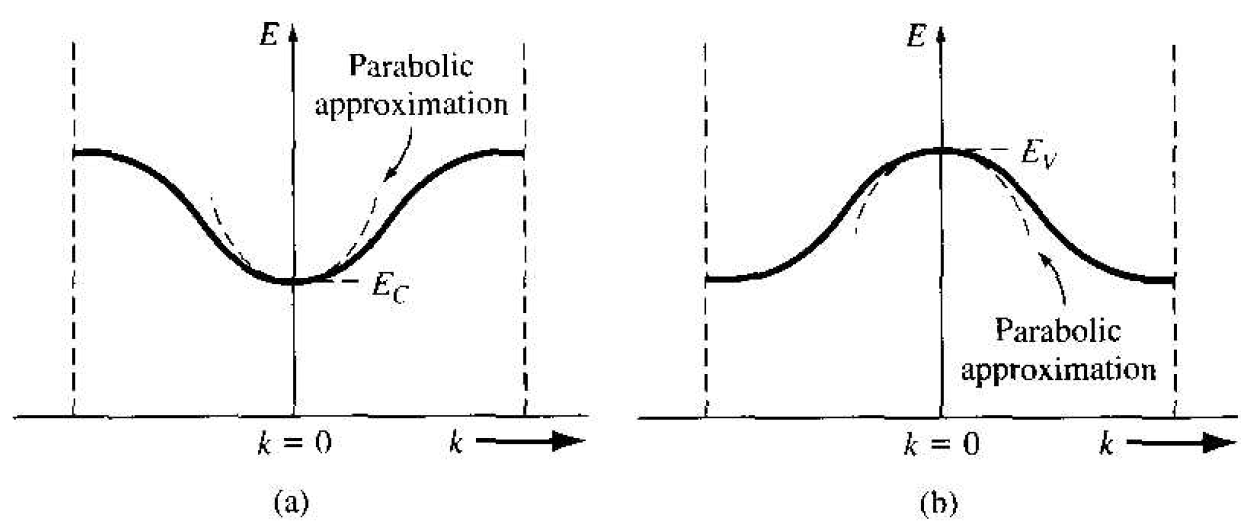
Figure 1.1  (a) The conduction band in reduced k space, and the parabolic approximation. (b) The valence band in reduced k space, and the parabolic approximation.

The energy E, is the energy at the bottom of the band. Since E > E_c, the parameter C₁ is a positive quantity.

Taking the second derivative of E with respect to k from Equation (9), we obtain

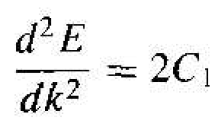(10)

We may put Equation (10) in the form

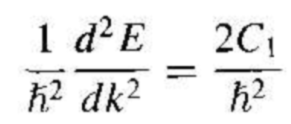(11)

Comparing Equation (11) with Equation(6), we may equate h²/2C₁ to the mass of the particle. However, the curvature of the curve in Figure 1.1a will not, in general, be the same as the curvature of the free-particle curve. We may write

(12)

where m* is called the effective mass. Since C₂ > 0, we have that m* > 0 also.

The effective mass is a parameter that relates the quantum mechanical results to the classical force equations. In most instances, the electron in the bottom of the conduction band can be thought of as a classical particle whose motion can be modeled by Newtonian mechanics, provided that the internal forces and quantum mechanical properties are taken into account through the effective mass. If we apply an electric field to the electron in the bottom of the allowed energy band, we may write the acceleration as

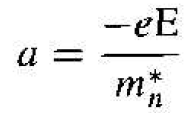(13)

where m^*_n is the effective mass of the electron. The effective mass m^*_n of the electron near the bottom of the conduction band is a constant.

مواضيع ذات صلة

CONDUCTORS

Concept of the Hole

Drift Current

The Energy Band and the Bond Model