


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 9-10-2019
Date: 25-4-2019
Date: 15-5-2018
|
A vector derivative is a derivative taken with respect to a vector field. Vector derivatives are extremely important in physics, where they arise throughout fluid mechanics, electricity and magnetism, elasticity, and many other areas of theoretical and applied physics.
The following table summarizes the names and notations for various vector derivatives.
| symbol | vector derivative |
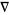 |
gradient |
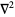 |
Laplacian or vector Laplacian |
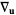 or or 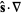 |
directional derivative |
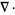 |
divergence |
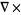 |
curl |
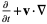 |
convective derivative |
Vector derivatives can be combined in different ways, producing sets of identities that are also very important in physics.
Vector derivative identities involving the curl include
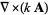 |
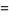 |
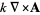 |
(1) |
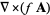 |
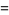 |
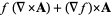 |
(2) |
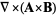 |
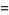 |
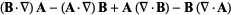 |
(3) |
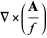 |
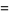 |
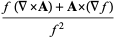 |
(4) |
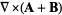 |
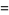 |
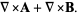 |
(5) |
In Cartesian coordinates
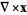 |
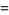 |
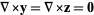 |
(6) |
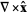 |
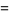 |
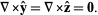 |
(7) |
In spherical coordinates,
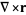 |
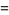 |
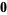 |
(8) |
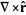 |
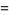 |
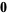 |
(9) |
![del x[rf(r)]](http://mathworld.wolfram.com/images/equations/VectorDerivative/Inline35.gif) |
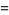 |
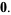 |
(10) |
Vector derivative identities involving the divergence include
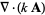 |
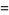 |
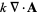 |
(11) |
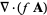 |
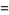 |
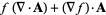 |
(12) |
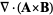 |
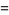 |
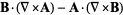 |
(13) |
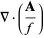 |
 |
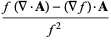 |
(14) |
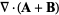 |
 |
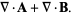 |
(15) |
In Cartesian coordinates,
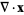 |
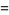 |
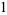 |
(16) |
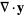 |
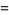 |
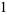 |
(17) |
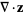 |
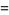 |
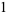 |
(18) |
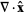 |
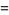 |
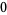 |
(19) |
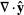 |
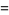 |
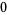 |
(20) |
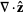 |
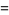 |
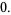 |
(21) |
In spherical coordinates,
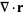 |
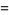 |
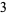 |
(22) |
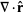 |
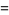 |
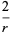 |
(23) |
![del ·[rf(r)]](http://mathworld.wolfram.com/images/equations/VectorDerivative/Inline77.gif) |
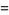 |
![partial/(partialx)[xf(r)]+partial/(partialy)[yf(r)]+partial/(partialz)[zf(r)]](http://mathworld.wolfram.com/images/equations/VectorDerivative/Inline79.gif) |
(24) |
![partial/(partialx)[xf(r)]](http://mathworld.wolfram.com/images/equations/VectorDerivative/Inline80.gif) |
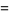 |
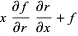 |
(25) |
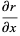 |
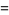 |
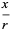 |
(26) |
![partial/(partialx)[xf(r)]](http://mathworld.wolfram.com/images/equations/VectorDerivative/Inline86.gif) |
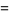 |
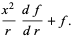 |
(27) |
By symmetry,
![del ·[rf(r)]](http://mathworld.wolfram.com/images/equations/VectorDerivative/Inline89.gif) |
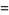 |
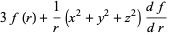 |
(28) |
 |
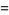 |
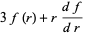 |
(29) |
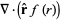 |
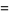 |
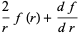 |
(30) |
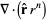 |
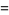 |
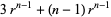 |
(31) |
 |
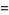 |
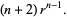 |
(32) |
Vector derivative identities involving the gradient include
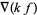 |
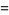 |
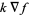 |
(33) |
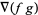 |
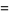 |
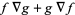 |
(34) |
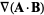 |
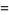 |
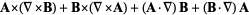 |
(35) |
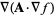 |
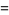 |
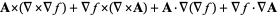 |
(36) |
 |
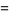 |
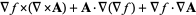 |
(37) |
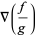 |
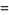 |
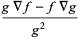 |
(38) |
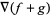 |
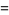 |
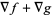 |
(39) |
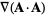 |
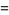 |
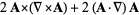 |
(40) |
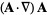 |
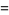 |
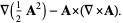 |
(41) |
Vector second derivative identities include
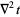 |
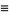 |
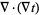 |
(42) |
 |
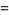 |
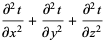 |
(43) |
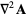 |
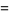 |
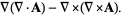 |
(44) |
This very important second derivative is known as the Laplacian.
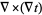 |
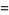 |
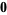 |
(45) |
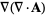 |
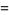 |
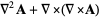 |
(46) |
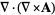 |
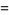 |
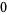 |
(47) |
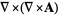 |
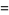 |
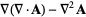 |
(48) |
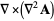 |
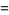 |
![del x[del (del ·A)]-del x[del x(del xA)]](http://mathworld.wolfram.com/images/equations/VectorDerivative/Inline154.gif) |
(49) |
 |
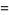 |
![-del x[del x(del xA)]](http://mathworld.wolfram.com/images/equations/VectorDerivative/Inline157.gif) |
(50) |
 |
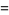 |
![-{del [del ·(del xA)]-del ^2(del xA)}](http://mathworld.wolfram.com/images/equations/VectorDerivative/Inline160.gif) |
(51) |
 |
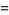 |
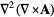 |
(52) |
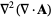 |
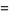 |
![del ·[del (del ·A)]](http://mathworld.wolfram.com/images/equations/VectorDerivative/Inline166.gif) |
(53) |
 |
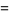 |
![del ·[del ^2A+del x(del xA)]](http://mathworld.wolfram.com/images/equations/VectorDerivative/Inline169.gif) |
(54) |
 |
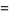 |
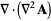 |
(55) |
![del ^2[del x(del xA)]](http://mathworld.wolfram.com/images/equations/VectorDerivative/Inline173.gif) |
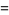 |
![del ^2[del (del ·A)-del ^2A]](http://mathworld.wolfram.com/images/equations/VectorDerivative/Inline175.gif) |
(56) |
 |
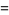 |
![del ^2[del (del ·A)]-del ^4A](http://mathworld.wolfram.com/images/equations/VectorDerivative/Inline178.gif) |
(57) |
![del x[del ^2(del xA)]](http://mathworld.wolfram.com/images/equations/VectorDerivative/Inline179.gif) |
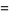 |
![del ^2[del (del ·A)]-del ^4A](http://mathworld.wolfram.com/images/equations/VectorDerivative/Inline181.gif) |
(58) |
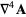 |
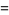 |
![-del ^2[del x(del xA)]+del ^2[del (del ·A)]](http://mathworld.wolfram.com/images/equations/VectorDerivative/Inline184.gif) |
(59) |
 |
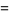 |
![del x[del ^2(del xA)]-del ^2[del x(del xA)].](http://mathworld.wolfram.com/images/equations/VectorDerivative/Inline187.gif) |
(60) |
Identities involving combinations of vector derivatives include
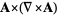 |
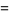 |
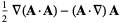 |
(61) |
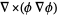 |
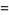 |
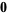 |
(62) |
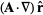 |
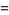 |
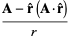 |
(63) |
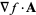 |
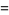 |
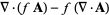 |
(64) |
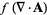 |
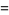 |
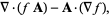 |
(65) |
where (64) and (65) follow from divergence rule (2).
REFERENCES:
Gradshteyn, I. S. and Ryzhik, I. M. "Vector Field Theorem." Ch. 10 in Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, pp. 1081-1092, 2000.
Morse, P. M. and Feshbach, H. "The Differential Operator 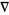 " and "Table of Useful Vector and Dyadic Equations." In Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 31-44, 50-54, and 114-115, 1953.
" and "Table of Useful Vector and Dyadic Equations." In Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 31-44, 50-54, and 114-115, 1953.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|