


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 11-6-2018
Date: 12-6-2018
Date: 22-6-2018
|
Any real function 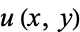 with continuous second partial derivatives which satisfies Laplace's equation,
with continuous second partial derivatives which satisfies Laplace's equation,
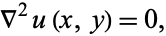 |
(1) |
is called a harmonic function. Harmonic functions are called potential functions in physics and engineering. Potential functions are extremely useful, for example, in electromagnetism, where they reduce the study of a 3-component vector field to a 1-component scalar function. A scalar harmonic function is called a scalar potential, and a vector harmonic function is called a vector potential.
To find a class of such functions in the plane, write the Laplace's equation in polar coordinates
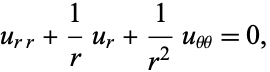 |
(2) |
and consider only radial solutions
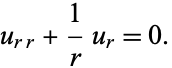 |
(3) |
This is integrable by quadrature, so define 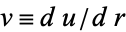 ,
,
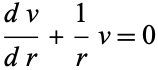 |
(4) |
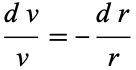 |
(5) |
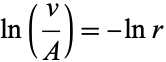 |
(6) |
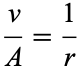 |
(7) |
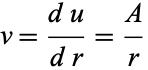 |
(8) |
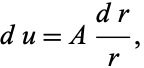 |
(9) |
so the solution is
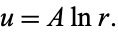 |
(10) |
Ignoring the trivial additive and multiplicative constants, the general pure radial solution then becomes
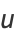 |
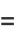 |
![ln[(x-a)^2+(y-b)^2]^(1/2)](http://mathworld.wolfram.com/images/equations/HarmonicFunction/Inline5.gif) |
(11) |
 |
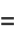 |
![1/2ln[(x-a)^2+(y-b)^2].](http://mathworld.wolfram.com/images/equations/HarmonicFunction/Inline8.gif) |
(12) |
Other solutions may be obtained by differentiation, such as
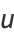 |
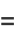 |
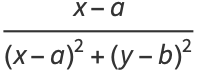 |
(13) |
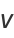 |
 |
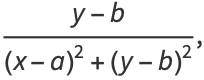 |
(14) |
 |
 |
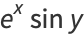 |
(15) |
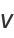 |
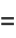 |
 |
(16) |
and
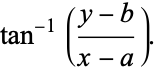 |
(17) |
Harmonic functions containing azimuthal dependence include
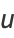 |
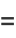 |
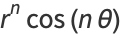 |
(18) |
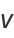 |
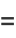 |
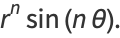 |
(19) |
The Poisson kernel
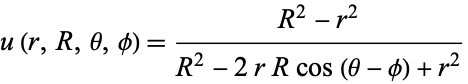 |
(20) |
is another harmonic function.
REFERENCES:
Ash, J. M. (Ed.). Studies in Harmonic Analysis. Washington, DC: Math. Assoc. Amer., 1976.
Axler, S.; Bourdon, P.; and Ramey, W. Harmonic Function Theory. Springer-Verlag, 1992.
Benedetto, J. J. Harmonic Analysis and Applications. Boca Raton, FL: CRC Press, 1996.
Cohn, H. Conformal Mapping on Riemann Surfaces. New York: Dover, 1980.
Krantz, S. G. "Harmonic Functions." §1.4.1 and Ch. 7 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 16 and 89-101, 1999.
Weisstein, E. W. "Books about Potential Theory." http://www.ericweisstein.com/encyclopedias/books/PotentialTheory.html.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|