المرجع الالكتروني للمعلوماتية
المرجع الألكتروني للمعلوماتية
ENGLISH
آخر المواضيع المضافة

الرياضيات
عدد المواضيع في هذا القسم 9761 موضوعاً
تاريخ الرياضيات
الرياضيات المتقطعة
الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
التحليل
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان

Untitled Document
أبحث عن شيء أخر المرجع الالكتروني للمعلوماتية
أضيف حديثاً
العينات غير العشوائية (غير الاحتمالية)- العينة العمدية (العينة القصدية) Sample Purposive
2025-01-12
العينات غير العشوائية (غير الاحتمالية)- العينة العرضية (العينة الصدفة) Accidental Sample
2025-01-12
السرعة المدارية Orbital Velocity
2025-01-12
الاسطرلاب
2025-01-12
ظهور التلسكوبات
2025-01-12
آثار فسخ عقد الزواج بعد الدخول بالنسبة للنفقة في قانون الاحوال الشخصية الكويتي
2025-01-12

وثائقيات
العباءة العربية .. إرث الآباء واعتزاز الأبناء
التاريخ / 20-09-2024

مختارات
كفارة الغيبة
29-9-2016
النوكليوزيدات والنوكليوتيدات هي مشتقات للبورينات والبيريميدينات
27-11-2021
المتحكمات اليدوية بالتعريض الضوئي
16-12-2021
The input to the Scottish Vowel Length Rule
2024-12-17
الانباط
13-11-2016
التصدير
25-03-2015

Mean-Value Property  
  
551   05:54 مساءً   date: 24-5-2018
Author : Krantz, S. G
Book or Source : "The Mean Value Property on Circles." §7.4.1 in Handbook of Complex Variables. Boston, MA: Birkhäuser
Page and Part : ...


Read More
Poisson Kernel
Date: 24-5-2018 981
Emden Differential Equation
Date: 11-6-2018 675
alerkin Method
Date: 21-5-2018 672

Mean-Value Property

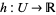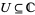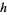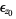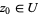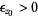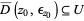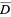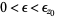Let a function h:U->R be continuous on an open set U subset= C. Then h is said to have the epsilon_(z_0)-property if, for each z_0 in U, there exists an epsilon_(z_0)>0 such that D^_(z_0,epsilon_(z_0)) subset= U, where D^_ is a closed disk, and for every 0<epsilon<epsilon_(z_0),

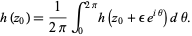h(z_0)=1/(2pi)int_0^(2pi)h(z_0+epsilone^(itheta))dtheta.

If 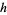h has the mean-value property, then 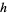h is harmonic.

REFERENCES:

Krantz, S. G. "The Mean Value Property on Circles." §7.4.1 in Handbook of Complex Variables. Boston, MA: Birkhäuser, p. 94, 1999.




الجبر أحد الفروع الرئيسية في الرياضيات، حيث إن التمكن من الرياضيات يعتمد على الفهم السليم للجبر. ويستخدم المهندسون والعلماء الجبر يومياً، وتعول المشاريع التجارية والصناعية على الجبر لحل الكثير من المعضلات التي تتعرض لها. ونظراً لأهمية الجبر في الحياة العصرية فإنه يدرّس في المدارس والجامعات في جميع أنحاء العالم. ويُعجب الكثير من الدارسين للجبر بقدرته وفائدته الكبيرتين، إذ باستخدام الجبر يمكن للمرء أن يحل كثيرًا من المسائل التي يتعذر حلها باستخدام الحساب فقط.وجاء اسمه من كتاب عالم الرياضيات والفلك والرحالة محمد بن موسى الخورازمي.


يعتبر علم المثلثات Trigonometry علماً عربياً ، فرياضيو العرب فضلوا علم المثلثات عن علم الفلك كأنهما علمين متداخلين ، ونظموه تنظيماً فيه لكثير من الدقة ، وقد كان اليونان يستعملون وتر CORDE ضعف القوسي قياس الزوايا ، فاستعاض رياضيو العرب عن الوتر بالجيب SINUS فأنت هذه الاستعاضة إلى تسهيل كثير من الاعمال الرياضية.

تعتبر المعادلات التفاضلية خير وسيلة لوصف معظم المـسائل الهندسـية والرياضـية والعلمية على حد سواء، إذ يتضح ذلك جليا في وصف عمليات انتقال الحرارة، جريان الموائـع، الحركة الموجية، الدوائر الإلكترونية فضلاً عن استخدامها في مسائل الهياكل الإنشائية والوصف الرياضي للتفاعلات الكيميائية.
ففي في الرياضيات, يطلق اسم المعادلات التفاضلية على المعادلات التي تحوي مشتقات و تفاضلات لبعض الدوال الرياضية و تظهر فيها بشكل متغيرات المعادلة . و يكون الهدف من حل هذه المعادلات هو إيجاد هذه الدوال الرياضية التي تحقق مشتقات هذه المعادلات.





الأخبار الصحية
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
التاريخ / 2025-01-09

الأخبار العلمية
القمر "يبتلع" المريخ!
التاريخ / 2025-01-09

الساحة الاسلامية
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
التاريخ / 2025-01-12