


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-6-2018
Date: 12-6-2018
Date: 26-12-2018
|
The associated Legendre differential equation is a generalization of the Legendre differential equation given by
![d/(dx)[(1-x^2)(dy)/(dx)]+[l(l+1)-(m^2)/(1-x^2)]y=0,](http://mathworld.wolfram.com/images/equations/AssociatedLegendreDifferentialEquation/NumberedEquation1.gif) |
(1) |
which can be written
![(1-x^2)(d^2y)/(dx^2)-2x(dy)/(dx)+[l(l+1)-(m^2)/(1-x^2)]y=0](http://mathworld.wolfram.com/images/equations/AssociatedLegendreDifferentialEquation/NumberedEquation2.gif) |
(2) |
(Abramowitz and Stegun 1972; Zwillinger 1997, p. 124). The solutions 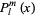 to this equation are called the associated Legendre polynomials (if
to this equation are called the associated Legendre polynomials (if 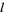 is an integer), or associated Legendre functions of the first kind (if
is an integer), or associated Legendre functions of the first kind (if 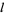 is not an integer). The complete solution is
is not an integer). The complete solution is
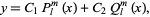 |
(3) |
where 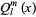 is a Legendre function of the second kind.
is a Legendre function of the second kind.
The associated Legendre differential equation is often written in a form obtained by setting 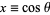 . Plugging the identities
. Plugging the identities
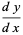 |
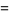 |
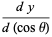 |
(4) |
 |
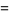 |
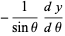 |
(5) |
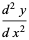 |
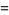 |
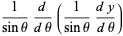 |
(6) |
 |
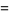 |
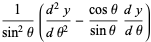 |
(7) |
into (◇) then gives
![((d^2y)/(dtheta^2)-(costheta)/(sintheta)(dy)/(dtheta))+2(costheta)/(sintheta)(dy)/(dtheta)+[l(l+1)-(m^2)/(sin^2theta)]y=0](http://mathworld.wolfram.com/images/equations/AssociatedLegendreDifferentialEquation/NumberedEquation4.gif) |
(8) |
![(d^2y)/(dtheta^2)+(costheta)/(sintheta)(dy)/(dtheta)+[l(l+1)-(m^2)/(sin^2theta)]y=0.](http://mathworld.wolfram.com/images/equations/AssociatedLegendreDifferentialEquation/NumberedEquation5.gif) |
(9 |
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 332, 1972.
Moon, P. and Spencer, D. E. Field Theory for Engineers. New York: Van Nostrand, 1961.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, 1997.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|