


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 27-12-2018
Date: 12-7-2018
Date: 13-6-2018
|
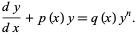 |
(1) |
Let 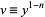 for
for 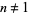 . Then
. Then
 |
(2) |
Rewriting (1) gives
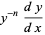 |
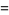 |
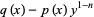 |
(3) |
 |
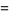 |
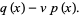 |
(4) |
Plugging (4) into (3),
![(dv)/(dx)=(1-n)[q(x)-vp(x)].](http://mathworld.wolfram.com/images/equations/BernoulliDifferentialEquation/NumberedEquation3.gif) |
(5) |
Now, this is a linear first-order ordinary differential equation of the form
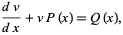 |
(6) |
where  and
and 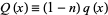 . It can therefore be solved analytically using an integrating factor
. It can therefore be solved analytically using an integrating factor
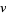 |
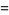 |
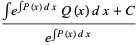 |
(7) |
 |
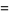 |
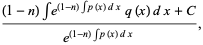 |
(8) |
where 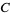 is a constant of integration. If
is a constant of integration. If 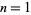 , then equation (◇) becomes
, then equation (◇) becomes
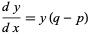 |
(9) |
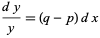 |
(10) |
![y=C_2e^(int[q(x)-p(x)]dx).](http://mathworld.wolfram.com/images/equations/BernoulliDifferentialEquation/NumberedEquation7.gif) |
(11) |
The general solution is then, with 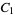 and
and 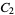 constants,
constants,
![y={[((1-n)inte^((1-n)intp(x)dx)q(x)dx+C_1)/(e^((1-n)intp(x)dx))]^(1/(1-n)) for n!=1; C_2e^(int[q(x)-p(x)]dx) for n=1.](http://mathworld.wolfram.com/images/equations/BernoulliDifferentialEquation/NumberedEquation8.gif) |
(12) |
REFERENCES:
Boyce, W. E. and DiPrima, R. C. Elementary Differential Equations and Boundary Value Problems, 5th ed. New York: Wiley, p. 28, 1992.
Ince, E. L. Ordinary Differential Equations. New York: Dover, p. 22, 1956.
Rainville, E. D. and Bedient, P. E. Elementary Differential Equations. New York: Macmillian, pp. 69-71, 1964.
Simmons, G. F. Differential Equations, With Applications and Historical Notes. New York: McGraw-Hill, p. 49, 1972.
Zwillinger, D. (Ed.). CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, p. 413, 1995.
Zwillinger, D. "Bernoulli Equation." §II.A.37 in Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, pp. 120 and 157-158, 1997.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|