


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-6-2018
Date: 21-5-2018
Date: 11-6-2018
|

Critical damping is a special case of damped simple harmonic motion
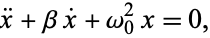 |
(1) |
in which
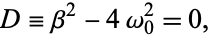 |
(2) |
where 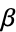 is the damping constant. Therefore
is the damping constant. Therefore
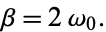 |
(3) |
In this case, 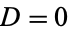 so the solutions of the form
so the solutions of the form 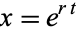 satisfy
satisfy
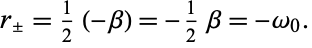 |
(4) |
One of the solutions is therefore
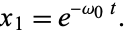 |
(5) |
In order to find the other linearly independent solution, we can make use of the identity
![x_2(t)=x_1(t)int(e^(-intp(t)dt))/([x_1(t)]^2)dt.](http://mathworld.wolfram.com/images/equations/CriticallyDampedSimpleHarmonicMotion/NumberedEquation6.gif) |
(6) |
Since we have 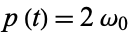 ,
, 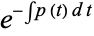 simplifies to
simplifies to 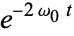 . Equation (6) therefore becomes
. Equation (6) therefore becomes
![x_2(t)=e^(-omega_0t)int(e^(-2omega_0t))/([e^(-omega_0t)]^2)dt=e^(-omega_0t)intdt=te^(-omega_0t).](http://mathworld.wolfram.com/images/equations/CriticallyDampedSimpleHarmonicMotion/NumberedEquation7.gif) |
(7) |
The general solution is therefore
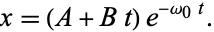 |
(8) |
In terms of the constants 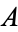 and
and 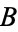 , the initial values are
, the initial values are
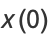 |
 |
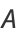 |
(9) |
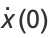 |
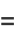 |
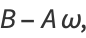 |
(10) |
so
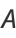 |
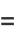 |
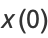 |
(11) |
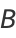 |
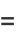 |
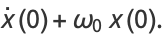 |
(12) |
The above plot shows a critically damped simple harmonic oscillator with 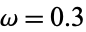 ,
, 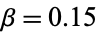 for a variety of initial conditions
for a variety of initial conditions 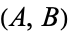 .
.
For sinusoidally forced simple harmonic motion with critical damping, the equation of motion is
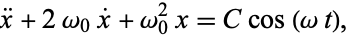 |
(13) |
and the Wronskian is
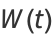 |
 |
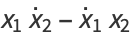 |
(14) |
 |
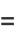 |
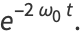 |
(15) |
Plugging this into the equation for the particular solution gives
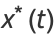 |
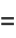 |
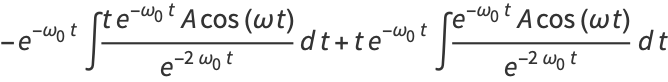 |
(16) |
 |
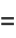 |
![A/((omega^2+omega_0^2)^2)[(omega_0^2-omega^2)cos(omegat)+2omegaomega_0sin(omegat)].](http://mathworld.wolfram.com/images/equations/CriticallyDampedSimpleHarmonicMotion/Inline35.gif) |
(17) |
Applying the harmonic addition theorem then gives
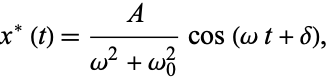 |
(18) |
where
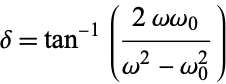 |
(19) |
REFERENCES:
Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, p. 528, 1984.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
قسم الشؤون الفكرية يقيم الحفل الختامي لمسابقة حفظ قصار السور للناشئة في أفريقيا
|
|
|