


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 30-5-2018
Date: 13-6-2018
Date: 30-5-2018
|
Adding a damping force proportional to  to the equation of simple harmonic motion, the first derivative of
to the equation of simple harmonic motion, the first derivative of  with respect to time, the equation of motion for damped simple harmonic motion is
with respect to time, the equation of motion for damped simple harmonic motion is
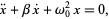 |
(1) |
where 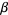 is the damping constant. This equation arises, for example, in the analysis of the flow of current in an electronic CLR circuit, (which contains a capacitor, an inductor, and a resistor). The curve produced by two damped harmonic oscillators at right angles to each other is called a harmonograph, and simplifies to a Lissajous curve if
is the damping constant. This equation arises, for example, in the analysis of the flow of current in an electronic CLR circuit, (which contains a capacitor, an inductor, and a resistor). The curve produced by two damped harmonic oscillators at right angles to each other is called a harmonograph, and simplifies to a Lissajous curve if 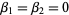 .
.
The damped harmonic oscillator can be solved by looking for trial solutions of the form 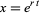 . Plugging this into (1) gives
. Plugging this into (1) gives
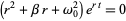 |
(2) |
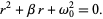 |
(3) |
This is a quadratic equation with solutions
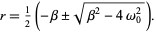 |
(4) |
There are therefore three solution regimes depending on the sign of the quantity inside the square root,
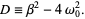 |
(5) |
The three regimes are summarized in the following table.
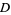 |
regime |
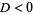 |
underdamping |
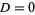 |
critical damping |
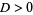 |
overdamping |
If a periodic (sinusoidal) forcing term is added at angular frequency 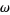 , the same three solution regimes are again obtained. Surprisingly, the resulting motion is still periodic (after an initial transient response, corresponding to the solution to the unforced case, has died out), but it has an amplitude different from the forcing amplitude.
, the same three solution regimes are again obtained. Surprisingly, the resulting motion is still periodic (after an initial transient response, corresponding to the solution to the unforced case, has died out), but it has an amplitude different from the forcing amplitude.
The particular solution 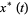 to the forced second-order nonhomogeneous ordinary differential equation
to the forced second-order nonhomogeneous ordinary differential equation
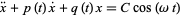 |
(6) |
due to forcing can be found using variation of parameters to be given by the equation
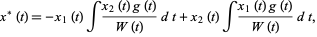 |
(7) |
where 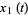 and
and 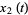 are the homogeneous solutions to the unforced equation
are the homogeneous solutions to the unforced equation
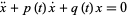 |
(8) |
and 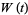 is the Wronskian of these two functions. Once the sinusoidal case of forcing is solved, it can then be generalized to any periodic function by expressing the periodic function in a Fourier series.
is the Wronskian of these two functions. Once the sinusoidal case of forcing is solved, it can then be generalized to any periodic function by expressing the periodic function in a Fourier series.
REFERENCES:
Papoulis, A. "Motion of a Harmonically Bound Particle." §15-2 in Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, pp. 524-528, 1984.



|
|
|
|
دراسة: حفنة من الجوز يوميا تحميك من سرطان القولون
|
|
|
|
|
|
|
تنشيط أول مفاعل ملح منصهر يستعمل الثوريوم في العالم.. سباق "الأرنب والسلحفاة"
|
|
|
|
|
|
|
الطلبة المشاركون: مسابقة فنِّ الخطابة تمثل فرصة للتنافس الإبداعي وتنمية المهارات
|
|
|