


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 3-7-2018
Date: 3-7-2018
Date: 27-5-2018
|
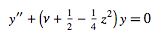 |
(1) |
whose solution is given by
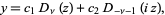 |
(2) |
where 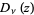 is a parabolic cylinder function.
is a parabolic cylinder function.
The generalized parabolic cylinder differential equation is the differential equation of the form
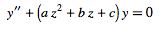 |
(3) |
(Abramowitz and Stegun 1972, p. 686; Zwillinger 1995, p. 414; Zwillinger 1997, p. 126) whose solution can be expressed in terms of parabolic cylinder functions as
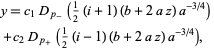 |
(4) |
where
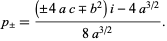 |
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Parabolic Cylinder Function." Ch. 19 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 685-700, 1972.
Zwillinger, D. (Ed.). CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, p. 414, 1995.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 126, 1997.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|