


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-5-2019
Date: 16-8-2018
Date: 19-5-2019
|
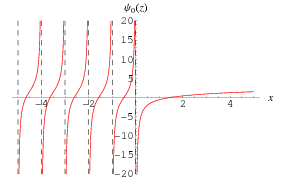
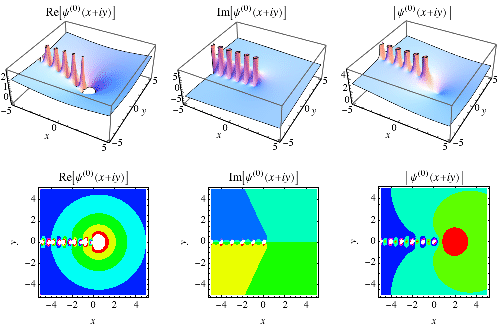 |
A special function which is given by the logarithmic derivative of the gamma function (or, depending on the definition, the logarithmic derivative of the factorial).
Because of this ambiguity, two different notations are sometimes (but not always) used, with
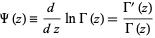 |
(1) |
defined as the logarithmic derivative of the gamma function 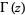 , and
, and
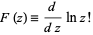 |
(2) |
defined as the logarithmic derivative of the factorial function. The two are connected by the relationship
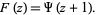 |
(3) |
The 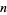 th derivative of
th derivative of 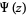 is called the polygamma function, denoted
is called the polygamma function, denoted 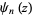 . The notation
. The notation
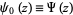 |
(4) |
is therefore frequently used for the digamma function itself, and Erdélyi et al. (1981) use the notation 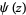 for
for 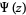 . The digamma function
. The digamma function 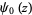 is returned by the function PolyGamma[z] or PolyGamma[0, z] in the Wolfram Language, and typeset using the notation
is returned by the function PolyGamma[z] or PolyGamma[0, z] in the Wolfram Language, and typeset using the notation 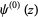 .
.
The digamma function arises in simple sums such as
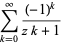 |
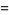 |
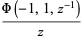 |
(5) |
 |
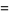 |
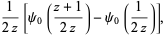 |
(6) |
where 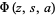 is a Lerch transcendent.
is a Lerch transcendent.
Special cases are given by
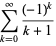 |
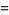 |
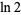 |
(7) |
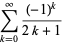 |
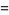 |
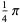 |
(8) |
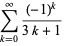 |
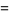 |
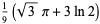 |
(9) |
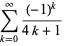 |
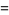 |
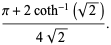 |
(10) |
Gauss's digamma theorem states that
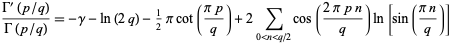 |
(11) |
(Allouche 1992, Knuth 1997, p. 94).
An asymptotic series for the digamma function is given by
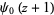 |
 |
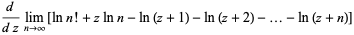 |
(12) |
 |
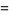 |
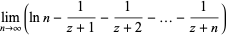 |
(13) |
 |
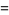 |
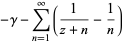 |
(14) |
 |
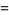 |
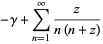 |
(15) |
 |
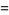 |
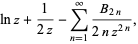 |
(16) |
where 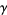 is the Euler-Mascheroni constant and
is the Euler-Mascheroni constant and 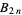 are Bernoulli numbers.
are Bernoulli numbers.
The digamma function satisfies
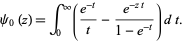 |
(17) |
For integer 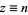 ,
,
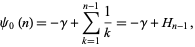 |
(18) |
where 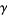 is the Euler-Mascheroni constant and
is the Euler-Mascheroni constant and 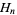 is a harmonic number.
is a harmonic number.
Other identities include
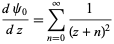 |
(19) |
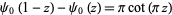 |
(20) |
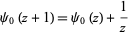 |
(21) |
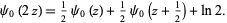 |
(22) |
Special values are
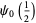 |
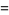 |
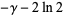 |
(23) |
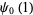 |
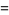 |
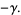 |
(24) |
At integer values,
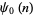 |
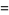 |
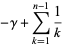 |
(25) |
 |
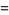 |
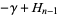 |
(26) |
(Derbyshire 2004, p. 58), and at half-integral values,
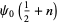 |
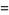 |
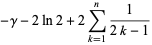 |
(27) |
 |
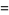 |
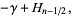 |
(28) |
where 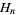 is a harmonic number.
is a harmonic number.
It is given by the unit square integral
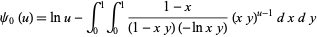 |
(29) |
for 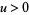 (Guillera and Sondow 2005). Plugging in
(Guillera and Sondow 2005). Plugging in 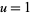 gives a special case involving the Euler-Mascheroni constant.
gives a special case involving the Euler-Mascheroni constant.
The series for 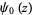 is given by
is given by
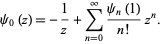 |
(30) |
A logarithmic series is given by
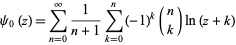 |
(31) |
(Guillera and Sondow 2005).
A surprising identity that arises from the FoxTrot series is given by
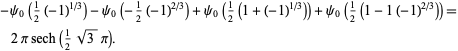 |
(32) |
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Psi (Digamma) Function." §6.3 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 258-259, 1972.
Allouche, J.-P. "Series and Infinite Products related to Binary Expansions of Integers." 1992. http://algo.inria.fr/seminars/sem92-93/allouche.ps.
Arfken, G. "Digamma and Polygamma Functions." §10.2 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 549-555, 1985.
Boros, G. and Moll, V. "The Psi Function." §10.11 in Irresistible Integrals: Symbolics, Analysis and Experiments in the Evaluation of Integrals. Cambridge, England: Cambridge University Press, pp. 212-215, 2004.
Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, 2004.
Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. "The 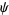 Function." §1.7 in Higher Transcendental Functions, Vol. 1.New York: Krieger, pp. 15-20, 1981.
Function." §1.7 in Higher Transcendental Functions, Vol. 1.New York: Krieger, pp. 15-20, 1981.
Guillera, J. and Sondow, J. "Double Integrals and Infinite Products for Some Classical Constants Via Analytic Continuations of Lerch's Transcendent." 16 June 2005 http://arxiv.org/abs/math.NT/0506319.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, 2003.
Jeffreys, H. and Jeffreys, B. S. "The Digamma (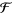 ) and Trigamma (
) and Trigamma (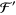 ) Functions." Methods of Mathematical Physics, 3rd ed.Cambridge, England: Cambridge University Press, pp. 465-466, 1988.
) Functions." Methods of Mathematical Physics, 3rd ed.Cambridge, England: Cambridge University Press, pp. 465-466, 1988.
Knuth, D. E. The Art of Computer Programming, Vol. 1: Fundamental Algorithms, 3rd ed. Reading, MA: Addison-Wesley, 1997.
Spanier, J. and Oldham, K. B. "The Digamma Function 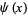 ." Ch. 44 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 423-434, 1987.
." Ch. 44 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 423-434, 1987.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|