


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-8-2018
Date: 18-9-2019
Date: 25-5-2019
|
 |
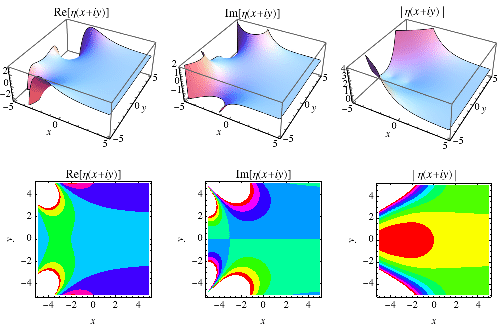 |
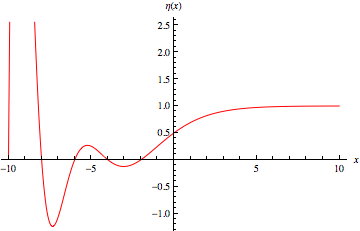
The Dirichlet eta function is the function 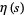 defined by
defined by
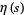 |
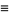 |
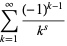 |
(1) |
 |
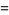 |
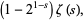 |
(2) |
where 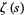 is the Riemann zeta function. Note that Borwein and Borwein (1987, p. 289) use the notation
is the Riemann zeta function. Note that Borwein and Borwein (1987, p. 289) use the notation 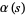 instead of
instead of 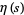 . The function is also known as the alternating zeta function and denoted
. The function is also known as the alternating zeta function and denoted 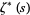 (Sondow 2003, 2005).
(Sondow 2003, 2005).
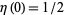 is defined by setting
is defined by setting 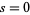 in the right-hand side of (2), while
in the right-hand side of (2), while 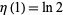 (sometimes called the alternating harmonic series) is defined using the left-hand side. The function vanishes at each zero of
(sometimes called the alternating harmonic series) is defined using the left-hand side. The function vanishes at each zero of 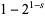 except
except 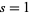 (Sondow 2003).
(Sondow 2003).
The eta function is related to the Riemann zeta function and Dirichlet lambda function by
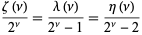 |
(3) |
and
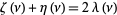 |
(4) |
(Spanier and Oldham 1987). The eta function is also a special case of the polylogarithm function,
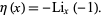 |
(5) |
The value 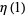 may be computed by noting that the Maclaurin series for
may be computed by noting that the Maclaurin series for 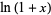 for
for 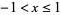 is
is
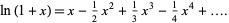 |
(6) |
Therefore, the natural logarithm of 2 is
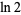 |
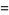 |
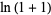 |
(7) |
 |
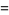 |
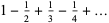 |
(8) |
 |
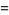 |
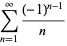 |
(9) |
 |
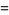 |
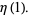 |
(10) |
The derivative of the eta function is given by
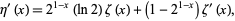 |
(11) |
or in the special case 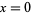 , by
, by
![lim_(x->0)[d/(dx)eta(x)]](http://mathworld.wolfram.com/images/equations/DirichletEtaFunction/Inline33.gif) |
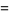 |
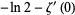 |
(12) |
 |
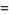 |
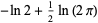 |
(13) |
 |
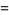 |
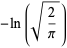 |
(14) |
 |
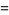 |
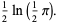 |
(15) |
This latter fact provides a remarkable proof of the Wallis formula.
Values for even integers are related to the analytical values of the Riemann zeta function. Particular values are given in Abramowitz and Stegun (1972, p. 811), and include
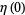 |
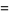 |
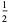 |
(16) |
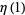 |
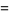 |
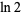 |
(17) |
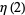 |
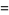 |
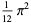 |
(18) |
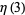 |
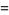 |
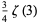 |
(19) |
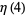 |
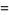 |
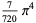 |
(20) |
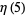 |
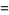 |
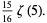 |
(21) |
It appears in the integral
![int_0^1int_0^1([-ln(xy)]^s)/(1+xy)dxdy=Gamma(s+2)eta(s+2)](http://mathworld.wolfram.com/images/equations/DirichletEtaFunction/NumberedEquation6.gif) |
(22) |
(Guillera and Sondow 2005).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 807-808, 1972.
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, 1987.
Guillera, J. and Sondow, J. "Double Integrals and Infinite Products for Some Classical Constants Via Analytic Continuations of Lerch's Transcendent." 16 June 2005. http://arxiv.org/abs/math.NT/0506319.
Havil, J. "Real Alternatives." §16.12 in Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 206-207, 2003.
Sondow, J. "Zeros of the Alternating Zeta Function on the Line ![R[s]=1](http://mathworld.wolfram.com/images/equations/DirichletEtaFunction/Inline63.gif) ." Amer. Math. Monthly 110, 435-437, 2003.
." Amer. Math. Monthly 110, 435-437, 2003.
Sondow, J. "Double Integrals for Euler's Constant and 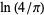 and an Analog of Hadjicostas's Formula." Amer. Math. Monthly112, 61-65, 2005.
and an Analog of Hadjicostas's Formula." Amer. Math. Monthly112, 61-65, 2005.
Spanier, J. and Oldham, K. B. "The Zeta Numbers and Related Functions." Ch. 3 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 25-33, 1987.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
قسم التطوير يقدم محاضرات عن نهج البلاغة في العتبة الكاظمية
|
|
|