


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 20-7-2019
Date: 9-9-2019
Date: 30-6-2019
|
The Leibniz integral rule gives a formula for differentiation of a definite integral whose limits are functions of the differential variable,
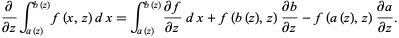 |
(1) |
It is sometimes known as differentiation under the integral sign.
This rule can be used to evaluate certain unusual definite integrals such as
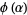 |
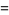 |
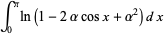 |
(2) |
 |
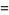 |
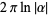 |
(3) |
for 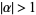 (Woods 1926).
(Woods 1926).
Feynman (1997, pp. 69-72) recalled seeing the method in Woods (1926) and remarked "So because I was self-taught using that book, I had peculiar methods for doing integrals," and "I used that one damn tool again and again."
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 11, 1972.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 232, 1987.
Boros, G. and Moll, V. Irresistible Integrals: Symbolics, Analysis and Experiments in the Evaluation of Integrals. Cambridge, England: Cambridge University Press, pp. 20-21, 2004.
Feynman, R. P. "A Different Set of Tools." In 'Surely You're Joking, Mr. Feynman!': Adventures of a Curious Character. New York: W. W. Norton, 1997.
Hijab, O. Introduction to Calculus and Classical Analysis. New York: Springer-Verlag, p. 189, 1997.
Kaplan, W. "Integrals Depending on a Parameter--Leibnitz's Rule." §4.9 in Advanced Calculus, 4th ed. Reading, MA: Addison-Wesley, pp. 256-258, 1992.
Woods, F. S. "Differentiation of a Definite Integral." §60 in Advanced Calculus: A Course Arranged with Special Reference to the Needs of Students of Applied Mathematics. Boston, MA: Ginn, pp. 141-144, 1926.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|