


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-10-2018
Date: 27-11-2018
Date: 18-11-2018
|
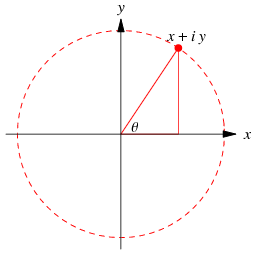
An Argand diagram is a plot of complex numbers as points
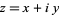 |
in the complex plane using the x-axis as the real axis and y-axis as the imaginary axis. In the plot above, the dashed circle represents the complex modulus 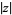 of
of 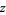 and the angle
and the angle 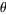 represents its complex argument.
represents its complex argument.
While Argand (1806) is generally credited with the discovery, the Argand diagram (also known as the Argand plane) was actually described by C. Wessel prior to Argand. Historically, the geometric representation of a complex number as a point in the plane was important because it made the whole idea of a complex number more acceptable. In particular, this visualization helped "imaginary" and "complex" numbers become accepted in mainstream mathematics as a natural extension to negative numbers along the real line.
REFERENCES:
Argand, R. Essai sur une manière de représenter les quantités imaginaires dans les constructions géométriques. Paris: Albert Blanchard, 1971. Reprint of the 2nd ed., published by G. J. Hoel in 1874. First edition published Paris, 1806.
Mazur, B. Imagining Numbers (Particularly the Square Root of Minus Fifteen). Farrar, Straus and Giroux, 2003.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 23, 1986.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
العتبة العباسية تستعدّ لتكريم عددٍ من الطالبات المرتديات للعباءة الزينبية في جامعات كركوك
|
|
|