


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 16-12-2018
Date: 18-10-2018
Date: 25-11-2018
|
A complex number may be taken to the power of another complex number. In particular, complex exponentiation satisfies
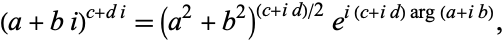 |
(1) |
where 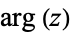 is the complex argument. Written explicitly in terms of real and imaginary parts,
is the complex argument. Written explicitly in terms of real and imaginary parts,
![(a+bi)^(c+di)=(a^2+b^2)^(c/2)e^(-darg(a+ib))×{cos[carg(a+ib)+1/2dln(a^2+b^2)]+isin[carg(a+ib)+1/2dln(a^2+b^2)]}.](http://mathworld.wolfram.com/images/equations/ComplexExponentiation/NumberedEquation2.gif) |
(2) |
An explicit example of complex exponentiation is given by
![(1+i)^(1+i)=sqrt(2)e^(-pi/4)[cos(1/4pi+1/2ln2)+isin(1/4pi+1/2ln2)].](http://mathworld.wolfram.com/images/equations/ComplexExponentiation/NumberedEquation3.gif) |
(3) |
A complex number taken to a complex number can be real. In fact, the famous example
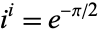 |
(4) |
shows that the power of the purely imaginary 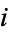 to itself is real.
to itself is real.
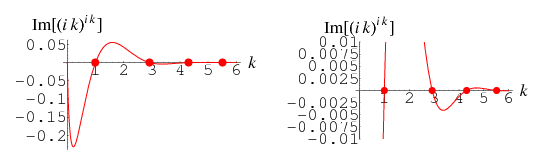
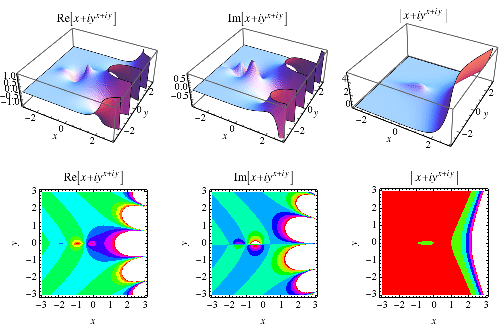 |
In fact, there is a family of values 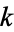 such that
such that 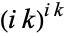 is real, as can be seen by writing
is real, as can be seen by writing
![(ik)^(ik)=e^(-kpi/2)[cos(klnk)+isin(klnk)].](http://mathworld.wolfram.com/images/equations/ComplexExponentiation/NumberedEquation5.gif) |
(5) |
This will be real when 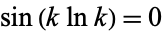 , i.e., for
, i.e., for
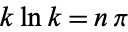 |
(6) |
for 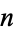 an integer. For positive
an integer. For positive 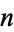 , this gives roots
, this gives roots 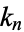 or
or
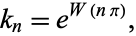 |
(7) |
where 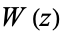 is the Lambert W-function. For
is the Lambert W-function. For 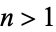 , this simplifies to
, this simplifies to
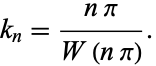 |
(8) |
For 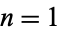 , 2, ..., these give the numeric values 1, 2.92606 (OEIS A088928), 4.30453, 5.51798, 6.63865, 7.6969, ....
, 2, ..., these give the numeric values 1, 2.92606 (OEIS A088928), 4.30453, 5.51798, 6.63865, 7.6969, ....
REFERENCES:
Sloane, N. J. A. Sequence A088928 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|