


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 8-3-2017
Date: 8-3-2017
Date: 11-3-2019
|
Let there be three polynomials 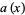 ,
, 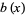 , and
, and 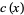 with no common factors such that
with no common factors such that
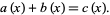 |
Then the number of distinct roots of the three polynomials is one or more greater than their largest degree. The theorem was first proved by Stothers (1981).
Mason's theorem may be viewed as a very special case of a Wronskian estimate (Chudnovsky and Chudnovsky 1984). The corresponding Wronskian identity in the proof by Lang (1993) is
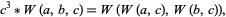 |
so if 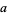 ,
, 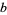 , and
, and 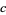 are linearly dependent, then so are
are linearly dependent, then so are 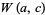 and
and 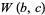 . More powerful Wronskian estimates with applications toward Diophantine approximation of solutions of linear differential equations may be found in Chudnovsky and Chudnovsky (1984) and Osgood (1985).
. More powerful Wronskian estimates with applications toward Diophantine approximation of solutions of linear differential equations may be found in Chudnovsky and Chudnovsky (1984) and Osgood (1985).
The rational function case of Fermat's last theorem follows trivially from Mason's theorem (Lang 1993, p. 195).
REFERENCES:
Chudnovsky, D. V. and Chudnovsky, G. V. "The Wronskian Formalism for Linear Differential Equations and Padé Approximations." Adv. Math. 53, 28-54, 1984.
Dubuque, W. "poly FLT, abc theorem, Wronskian formalism [was: Entire solutions of f^2+g^2=1]." math-fun@cs.arizona.edu posting, Jul 17, 1996.
Lang, S. "Old and New Conjectured Diophantine Inequalities." Bull. Amer. Math. Soc. 23, 37-75, 1990.
Lang, S. Algebra, 3rd ed. Reading, MA: Addison-Wesley, 1993.
Mason, R. C. Diophantine Equations over Functions Fields. Cambridge, England: Cambridge University Press, 1984.
Osgood, C. F. "Sometimes Effective Thue-Siegel-Roth-Schmidt-Nevanlinna Bounds, or Better." J. Number Th. 21, 347-389, 1985.
Stothers, W. W. "Polynomial Identities and Hauptmodulen." Quart. J. Math. Oxford Ser. II 32, 349-370, 1981.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
العتبة العباسية تستعدّ لتكريم عددٍ من الطالبات المرتديات للعباءة الزينبية في جامعات كركوك
|
|
|