


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 11-3-2019
Date: 19-1-2019
Date: 19-1-2019
|
A primitive polynomial is a polynomial that generates all elements of an extension field from a base field. Primitive polynomials are also irreducible polynomials. For any prime or prime power 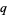 and any positive integer
and any positive integer 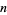 , there exists a primitive polynomial of degree
, there exists a primitive polynomial of degree 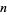 over GF(
over GF(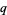 ). There are
). There are
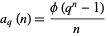 |
(1) |
primitive polynomials over GF( ), where
), where  is the totient function.
is the totient function.
A polynomial of degree  over the finite field GF(2) (i.e., with coefficients either 0 or 1) is primitive if it has polynomial order
over the finite field GF(2) (i.e., with coefficients either 0 or 1) is primitive if it has polynomial order 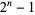 . For example,
. For example, 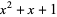 has order 3 since
has order 3 since
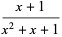 |
 |
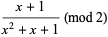 |
(2) |
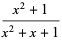 |
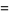 |
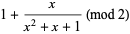 |
(3) |
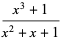 |
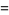 |
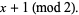 |
(4) |
Plugging in 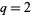 to equation (◇), the numbers of primitive polynomials over GF(2) are
to equation (◇), the numbers of primitive polynomials over GF(2) are
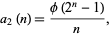 |
(5) |
giving 1, 1, 2, 2, 6, 6, 18, 16, 48, ... (OEIS A011260) for 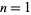 , 2, .... The following table lists the primitive polynomials (mod 2) of orders 1 through 5.
, 2, .... The following table lists the primitive polynomials (mod 2) of orders 1 through 5.
 |
primitive polynomials |
| 1 | 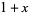 |
| 2 | 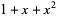 |
| 3 | 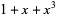 , , 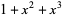 |
| 4 | 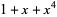 , , 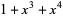 |
| 5 | 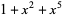 , , 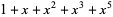 , , 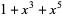 , , 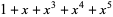 , , 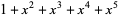 , ,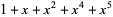 |
Amazingly, primitive polynomials over GF(2) define a recurrence relation which can be used to obtain a new pseudorandom bit from the 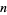 preceding ones.
preceding ones.
REFERENCES:
Berlekamp, E. R. Algebraic Coding Theory. New York: McGraw-Hill, p. 84, 1968.
Booth, T. L. "An Analytical Representation of Signals in Sequential Networks." In Proceedings of the Symposium on Mathematical Theory of Automata. New York, N.Y., April 24, 25, 26, 1962. Brooklyn, NY: Polytechnic Press of Polytechnic Inst. of Brooklyn, pp. 301-324, 1963.
Church, R. "Tables of Irreducible Polynomials for the First Four Prime Moduli." Ann. Math. 36, 198-209, 1935.
Fan, P. and Darnell, M. Table 5.1 in Sequence Design for Communications Applications. New York: Wiley, p. 118, 1996.
O'Connor, S. E. "Computing Primitive Polynomials." http://seanerikoconnor.freeservers.com/Mathematics/AbstractAlgebra/PrimitivePolynomials/overview.html.
Peterson, W. W. and Weldon, E. J. Jr. Error-Correcting Codes, 2nd ed. Cambridge, MA: MIT Press, p. 476, 1972.
Ristenblatt, M. P. "Pseudo-Random Binary Coded Waveforms." In Modern Radar (Ed. R. S. Berkowitz). New York: Wiley, pp. 274-314, 1965.
Ruskey, F. "Information on Primitive and Irreducible Polynomials." http://www.theory.csc.uvic.ca/~cos/inf/neck/PolyInfo.html.
Sloane, N. J. A. Sequence A011260/M0107 in "The On-Line Encyclopedia of Integer Sequences."
Zierler, N. and Brillhart, J. "On Primitive Trinomials." Inform. Control 13, 541-544, 1968.
Zierler, N. and Brillhart, J. "On Primitive Trinomials (II)." Inform. Control 14, 566-569, 1969.



|
|
|
|
هل تعرف كيف يؤثر الطقس على ضغط إطارات سيارتك؟ إليك الإجابة
|
|
|
|
|
|
|
معهد القرآن الكريم النسوي يقدم خدماته لزائري الإمام الكاظم (عليه السلام)
|
|
|