


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-3-2019
Date: 13-3-2019
Date: 13-3-2019
|
The asymptotic series for the gamma function is given by
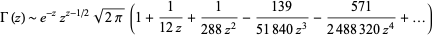 |
(1) |
(OEIS A001163 and A001164).
The coefficient 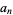 of
of 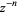 can given explicitly by
can given explicitly by
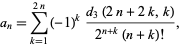 |
(2) |
where 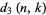 is the number of permutations of
is the number of permutations of  with
with  permutation cycles all of which are
permutation cycles all of which are  (Comtet 1974, p. 267). Another formula for the
(Comtet 1974, p. 267). Another formula for the 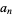 s is given by the recurrence relation
s is given by the recurrence relation
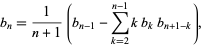 |
(3) |
with 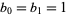 , then
, then
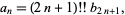 |
(4) |
where 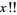 is the double factorial (Borwein and Corless 1999).
is the double factorial (Borwein and Corless 1999).
The series for 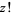 is obtained by adding an additional factor of
is obtained by adding an additional factor of 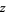 ,
,
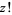 |
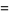 |
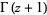 |
(5) |
 |
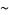 |
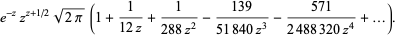 |
(6) |
The expansion of 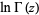 is what is usually called Stirling's series. It is given by the simple analytic expression
is what is usually called Stirling's series. It is given by the simple analytic expression
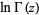 |
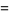 |
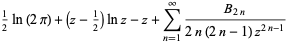 |
(7) |
 |
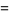 |
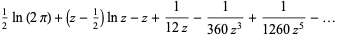 |
(8) |
(OEIS A046968 and A046969), where 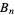 is a Bernoulli number. Interestingly, while the numerators in this expansion are the same as those of
is a Bernoulli number. Interestingly, while the numerators in this expansion are the same as those of 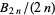 for the first several hundred terms, they differ at
for the first several hundred terms, they differ at 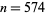 , 1185, 1240, 1269, 1376, 1906, 1910, ... (OEIS A090495), with the corresponding ratios being 37, 103, 37, 59, 131, 37, 67, ... (OEIS A090496).
, 1185, 1240, 1269, 1376, 1906, 1910, ... (OEIS A090495), with the corresponding ratios being 37, 103, 37, 59, 131, 37, 67, ... (OEIS A090496).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 257, 1972.
Arfken, G. "Stirling's Series." §10.3 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 555-559, 1985.
Borwein, J. M. and Corless, R. M. "Emerging Tools for Experimental Mathematics." Amer. Math. Monthly 106, 899-909, 1999.
Comtet, L. Advanced Combinatorics: The Art of Finite and Infinite Expansions, rev. enl. ed. Dordrecht, Netherlands: Reidel, p. 267, 1974.
Conway, J. H. and Guy, R. K. "Stirling's Formula." In The Book of Numbers. New York: Springer-Verlag, pp. 260-261, 1996.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 86-88, 2003.
Marsaglia, G. and Marsaglia, J. C. "A New Derivation of Stirling's Approximation to 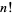 ." Amer. Math. Monthly 97, 826-829, 1990.
." Amer. Math. Monthly 97, 826-829, 1990.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, p. 443, 1953.
Sloane, N. J. A. Sequences A001163/M5400, A001164/M4878, A046968, A046969, A090495, and A090496 in "The On-Line Encyclopedia of Integer Sequences."
Uhler, H. S. "The Coefficients of Stirling's Series for 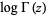 ." Proc. Nat. Acad. Sci. U.S.A. 28, 59-62, 1942.
." Proc. Nat. Acad. Sci. U.S.A. 28, 59-62, 1942.
Wrench, J. W. Jr. "Concerning Two Series for the Gamma Function." Math. Comput. 22, 617-626, 1968.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
العتبة العباسية تستعدّ لتكريم عددٍ من الطالبات المرتديات للعباءة الزينبية في جامعات كركوك
|
|
|