Exponential Growth

Exponential growth is the increase in a quantity 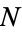 according to the law

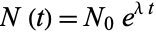(1)

for a parameter 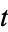 and constant  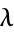(the analog of the decay constant), where  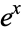is the exponential function and  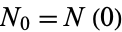is the initial value. Exponential growth is common in physical processes such as population growth in the absence of predators or resource restrictions (where a slightly more general form is known as the law of growth). Exponential growth also occurs as the limit of discrete processes such as compound interest.

Exponential growth is described by the first-order ordinary differential equation

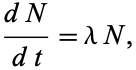(2)

which can be rearranged to

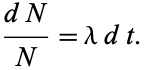(3)

Integrating both sides then gives

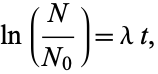(4)

and exponentiating both sides yields the functional form (1).

A much more antiquated term for population growth modeled according to an exponential equation is the so-called Malthusian equation, a result of a 1798 philosophical text by Thomas Malthus which investigated population dynamics under the assumption that the growth of the human population obeys a sort of exponential growth.

REFERENCES:

Malthus, T. R. "An Essay on the Principle of Population." 1798. http://www.econlib.org/library/Malthus/malPop.html.