


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-5-2019
Date: 30-3-2019
Date: 21-9-2018
|
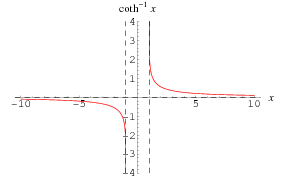
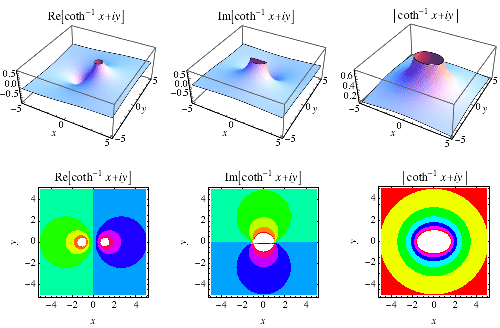 |
The inverse hyperbolic cotangent 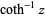 (Beyer 1987, p. 181; Zwillinger 1995, p. 481), sometimes called the area hyperbolic cotangent (Harris and Stocker 1998, p. 267), is the multivalued function that is the inverse function of the hyperbolic cotangent.
(Beyer 1987, p. 181; Zwillinger 1995, p. 481), sometimes called the area hyperbolic cotangent (Harris and Stocker 1998, p. 267), is the multivalued function that is the inverse function of the hyperbolic cotangent.
The variants 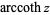 and
and 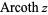 (Harris and Stocker 1998, p. 263) are sometimes used to refer to explicit principal values of the inverse hyperbolic cotangent, although this distinction is not always made. Worse yet, the notation
(Harris and Stocker 1998, p. 263) are sometimes used to refer to explicit principal values of the inverse hyperbolic cotangent, although this distinction is not always made. Worse yet, the notation 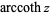 is sometimes used for the principal value, with
is sometimes used for the principal value, with 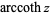 being used for the multivalued function (Abramowitz and Stegun 1972, p. 87). The function is sometimes denoted
being used for the multivalued function (Abramowitz and Stegun 1972, p. 87). The function is sometimes denoted 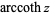 (Jeffrey 2000, p. 124) or
(Jeffrey 2000, p. 124) or 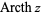 (Gradshteyn and Ryzhik 2000, p. xxx). Note that in the notation
(Gradshteyn and Ryzhik 2000, p. xxx). Note that in the notation 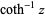 ,
, 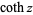 is the hyperbolic tangent and the superscript
is the hyperbolic tangent and the superscript 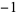 denotes an inverse function, not the multiplicative inverse.
denotes an inverse function, not the multiplicative inverse.
The principal value of 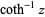 is implemented in the Wolfram Language as ArcCoth[z]
is implemented in the Wolfram Language as ArcCoth[z]
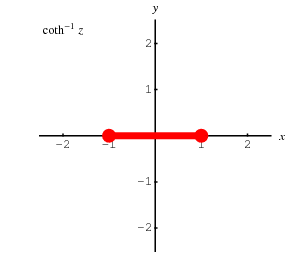
The inverse hyperbolic cotangent is a multivalued function and hence requires a branch cut in the complex plane, which the Wolfram Language's convention places at the line segment ![[-1,1]](http://mathworld.wolfram.com/images/equations/InverseHyperbolicCotangent/Inline12.gif) . This follows from the definition of
. This follows from the definition of 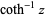 as
as
![coth^(-1)z=1/2[ln(1+1/z)-ln(1-1/z)].](http://mathworld.wolfram.com/images/equations/InverseHyperbolicCotangent/NumberedEquation1.gif) |
(1) |
The inverse hyperbolic cotangent is given in terms of the inverse cotangent by
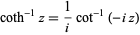 |
(2) |
(Gradshteyn and Ryzhik 2000, p. xxx). For 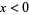 or
or 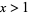 , this simplifies to
, this simplifies to
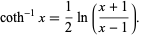 |
(3) |
The derivative is
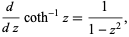 |
(4) |
and its indefinite integral is
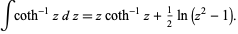 |
(5) |
It has the special values
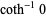 |
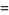 |
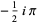 |
(6) |
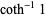 |
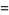 |
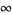 |
(7) |
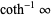 |
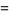 |
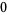 |
(8) |
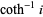 |
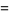 |
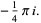 |
(9) |
It has series expansions
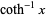 |
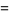 |
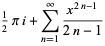 |
(10) |
 |
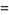 |
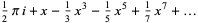 |
(11) |
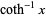 |
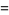 |
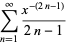 |
(12) |
 |
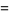 |
 |
(13) |
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Inverse Hyperbolic Functions." §4.6 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 86-89, 1972.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 142-143, 1987.
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, p. xxx, 2000.
Harris, J. W. and Stocker, H. Handbook of Mathematics and Computational Science. New York: Springer-Verlag, 1998.
Jeffrey, A. "Inverse Trigonometric and Hyperbolic Functions." §2.7 in Handbook of Mathematical Formulas and Integrals, 2nd ed.Orlando, FL: Academic Press, pp. 124-128, 2000.
Sloane, N. J. A. Sequence A005408/M2400 in "The On-Line Encyclopedia of Integer Sequences."
Spanier, J. and Oldham, K. B. "Inverse Trigonometric Functions." Ch. 35 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 331-341, 1987.
Zwillinger, D. (Ed.). "Inverse Hyperbolic Functions." §6.8 in CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, pp. 481-483, 1995.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|