المرجع الالكتروني للمعلوماتية
المرجع الألكتروني للمعلوماتية
ENGLISH
آخر المواضيع المضافة

الرياضيات
عدد المواضيع في هذا القسم 9761 موضوعاً
تاريخ الرياضيات
الرياضيات المتقطعة
الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
التحليل
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان

Untitled Document
أبحث عن شيء أخر المرجع الالكتروني للمعلوماتية
أضيف حديثاً
الشكر قناة موصلة للنعم الإلهية
2025-01-12
أسباب ودوافع الكفران وطرق علاجه
2025-01-12
عواقب كفران النعمة
2025-01-12
معنى كفران النعمة
2025-01-12
دور الإدارة الحكوميـة فـي التنـميـة التكـنولوجـيـة 2
2025-01-12
دور الإدارة الحكوميـة فـي التنـميـة التكـنولوجـيـة 1
2025-01-12

وثائقيات
العباءة العربية .. إرث الآباء واعتزاز الأبناء
التاريخ / 20-09-2024

مختارات
المجلات الالكترونية واعلاناتها المبوبة
8/9/2022
Confluent
22-1-2022
منع الاشخاص من الايمان برسول اللّه
4-5-2017
اهتمام الإنسان بالمحسوسات
2023-10-24
خصائص العلاقات الصحيحة بين الزوج والزوجة
7-7-2022
تأثير درجات الحرارة على أشجار الموالح
26-8-2022

Natural Logarithm of 10  
  
1836   03:49 مساءً   date: 25-6-2019
Author : Sloane, N. J. A.
Book or Source : Sequence A002392/M0394 in "The On-Line Encyclopedia of Integer Sequences."
Page and Part : ...


Read More
Weierstrass Sigma Function
Date: 23-4-2019 1695
Log Cosine Function
Date: 23-6-2019 1203
Normal Order
Date: 19-9-2018 1529

Natural Logarithm of 10

The decimal expansion of the natural logarithm of 10 is given by

 

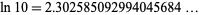ln10=2.302585092994045684...

(1)

(OEIS A002392).

It is also given by the BBP-type formulas

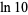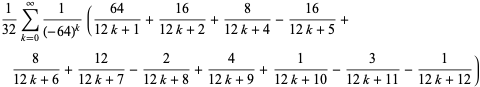ln10 = 1/(32)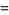sum_(k=0)^(infty)1/((-64)^k)((64)/(12k+1)+(16)/(12k+2)+8/(12k+4)-(16)/(12k+5)+8/(12k+6)+(12)/(12k+7)-2/(12k+8)+4/(12k+9)+1/(12k+10)-3/(12k+11)-1/(12k+12))

(2)
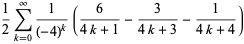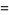= 1/2sum_(k=0)^(infty)1/((-4)^k)(6/(4k+1)-3/(4k+3)-1/(4k+4))

(3)
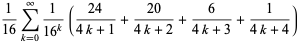= 1/(16)sum_(k=0)^(infty)1/(16^k)((24)/(4k+1)+(20)/(4k+2)+6/(4k+3)+1/(4k+4))

(4)
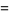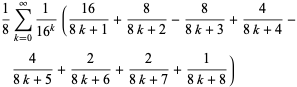= 1/8sum_(k=0)^(infty)1/(16^k)((16)/(8k+1)+8/(8k+2)-8/(8k+3)+4/(8k+4)-4/(8k+5)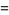+2/(8k+6)+2/(8k+7)+1/(8k+8))

(5)
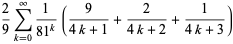= 2/9sum_(k=0)^(infty)1/(81^k)(9/(4k+1)+2/(4k+2)+1/(4k+3))

(6)
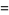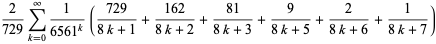= 2/(729)sum_(k=0)^(infty)1/(6561^k)((729)/(8k+1)+(162)/(8k+2)+(81)/(8k+3)+9/(8k+5)+2/(8k+6)+1/(8k+7))

(7)

(E. W. Weisstein, Aug. 28, 2008).

REFERENCES:

Sloane, N. J. A. Sequence A002392/M0394 in "The On-Line Encyclopedia of Integer Sequences."

Mansell, W. E. Tables of Natural and Common Logarithms. Royal Society Mathematical Tables, Vol. 8. Cambridge, England: Cambridge University Press, p. 2, 1964.

Uhler, H. S. "Recalculation and Extension of the Modulus and of the Logarithms of 2, 3, 5, 7 and 17." Proc. Nat. Acad. Sci. U. S. A. 26, 205-212, 1940.




الجبر أحد الفروع الرئيسية في الرياضيات، حيث إن التمكن من الرياضيات يعتمد على الفهم السليم للجبر. ويستخدم المهندسون والعلماء الجبر يومياً، وتعول المشاريع التجارية والصناعية على الجبر لحل الكثير من المعضلات التي تتعرض لها. ونظراً لأهمية الجبر في الحياة العصرية فإنه يدرّس في المدارس والجامعات في جميع أنحاء العالم. ويُعجب الكثير من الدارسين للجبر بقدرته وفائدته الكبيرتين، إذ باستخدام الجبر يمكن للمرء أن يحل كثيرًا من المسائل التي يتعذر حلها باستخدام الحساب فقط.وجاء اسمه من كتاب عالم الرياضيات والفلك والرحالة محمد بن موسى الخورازمي.


يعتبر علم المثلثات Trigonometry علماً عربياً ، فرياضيو العرب فضلوا علم المثلثات عن علم الفلك كأنهما علمين متداخلين ، ونظموه تنظيماً فيه لكثير من الدقة ، وقد كان اليونان يستعملون وتر CORDE ضعف القوسي قياس الزوايا ، فاستعاض رياضيو العرب عن الوتر بالجيب SINUS فأنت هذه الاستعاضة إلى تسهيل كثير من الاعمال الرياضية.

تعتبر المعادلات التفاضلية خير وسيلة لوصف معظم المـسائل الهندسـية والرياضـية والعلمية على حد سواء، إذ يتضح ذلك جليا في وصف عمليات انتقال الحرارة، جريان الموائـع، الحركة الموجية، الدوائر الإلكترونية فضلاً عن استخدامها في مسائل الهياكل الإنشائية والوصف الرياضي للتفاعلات الكيميائية.
ففي في الرياضيات, يطلق اسم المعادلات التفاضلية على المعادلات التي تحوي مشتقات و تفاضلات لبعض الدوال الرياضية و تظهر فيها بشكل متغيرات المعادلة . و يكون الهدف من حل هذه المعادلات هو إيجاد هذه الدوال الرياضية التي تحقق مشتقات هذه المعادلات.





الأخبار الصحية
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
التاريخ / 2025-01-12

الأخبار العلمية
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
التاريخ / 2025-01-12

الساحة الاسلامية
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
التاريخ / 2025-01-12