Power Mean

A power mean is a mean of the form

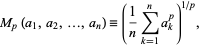(1)

where the parameter 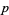 is an affinely extended real number and all 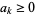. A power mean is also known as a generalized mean, Hölder mean, mean of degree (or order or power) 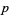, or power mean.

The following table summarizes some common named means that are special cases of the generalized mean, where

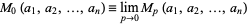(2)

and

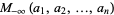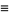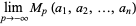			(3)
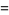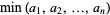			(4)
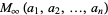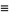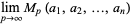			(5)
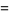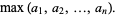			(6)

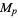	symbol	mean
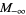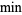		minimum
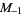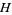		harmonic mean
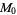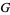		geometric mean
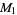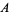		arithmetic mean
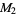	RMS	root-mean-square
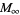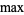		maximum

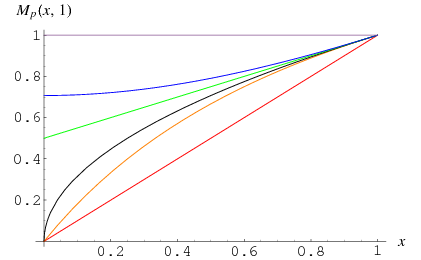
The plots above visualize the generalized mean by plotting the special values

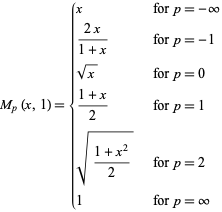(7)

with 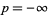 red, 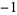 orange, 0 black, 1 green, 2 blue, and  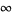violet.

REFERENCES:

Borwein, J. M. and Borwein, P. B. "General Means and Iterations." Ch. 8 in Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, 1987.

Bullen, P. S. "The Power Means." Ch. 3 in Handbook of Means and Their Inequalities. Dordrecht, Netherlands: Kluwer, 2003.

Hardy, G. H.; Littlewood, J. E.; and Pólya, G. Inequalities. Cambridge, England: Cambridge University Press, 1952.

Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, p. 121, 2003.