المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Oblate Spheroidal Wave Function |
 1441
 05:19 مساءً
date: 22-7-2019 |
Author : Abramowitz, M. and Stegun, I. A. 
Book or Source : "Spheroidal Wave Functions." Ch. 21 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York:... 
Page and Part : ...|
Read More
Date: 6-8-2019
3307
Date: 17-9-2018
1505
Date: 24-9-2019
1752
|
The wave equation in oblate spheroidal coordinates is
![del ^2Phi+k^2Phi=partial/(partialxi_1)[(xi_1^2+1)(partialPhi)/(partialxi_1)]
+partial/(partialxi_2)[(1-xi_2^2)(partialPhi)/(partialxi_2)]+(xi_1^2+xi_2^2)/((xi_1^2+1)(1-x_2^2))(partial^2Phi)/(partialphi^2)
+c^2(xi_1^2+xi_2^2)Phi=0,](http://mathworld.wolfram.com/images/equations/OblateSpheroidalWaveFunction/NumberedEquation1.gif) |
(1) |
where
 |
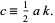(2) |
Substitute in a trial solution
 |
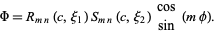(3) |
The radial differential equation is
![d/(dxi_2)[(1+xi_2^2)d/(dxi_2)S_(mn)(c,xi_2)]-(lambda_(mn)-c^2xi_2^2+(m^2)/(1+xi_2^2))R_(mn)(c,xi_2)=0,](http://mathworld.wolfram.com/images/equations/OblateSpheroidalWaveFunction/NumberedEquation4.gif) |
(4) |
and the angular differential equation is
![d/(dxi_2)[(1-xi_2^2)d/(dxi_2)S_(mn)(c,xi_2)]-(lambda_(mn)-c^2xi_2^2+(m^2)/(1-xi_2^2))R_(mn)(c,xi_2)=0](http://mathworld.wolfram.com/images/equations/OblateSpheroidalWaveFunction/NumberedEquation5.gif) |
(5) |
(Abramowitz and Stegun 1972, pp. 753-755; Zwillinger 1997, p. 127).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Spheroidal Wave Functions." Ch. 21 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 751-759, 1972.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 127, 1997.
|
|
|
|
دراسة: حفنة من الجوز يوميا تحميك من سرطان القولون
|
|
|
|
|
|
|
تنشيط أول مفاعل ملح منصهر يستعمل الثوريوم في العالم.. سباق "الأرنب والسلحفاة"
|
|
|
|
|
|
|
الطلبة المشاركون: مسابقة فنِّ الخطابة تمثل فرصة للتنافس الإبداعي وتنمية المهارات
|
|
|
