


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 2-5-2019
Date: 11-6-2019
Date: 3-6-2019
|
 |
For a real positive  , the Riemann-Siegel
, the Riemann-Siegel  function is defined by
function is defined by
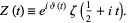 |
(1) |
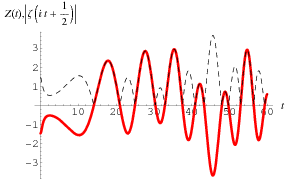
This function is sometimes also called the Hardy function or Hardy 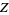 -function (Karatsuba and Voronin 1992, Borwein et al. 1999). The top plot superposes
-function (Karatsuba and Voronin 1992, Borwein et al. 1999). The top plot superposes 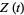 (thick line) on
(thick line) on 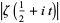 , where
, where 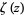 is the Riemann zeta function.
is the Riemann zeta function.
 |
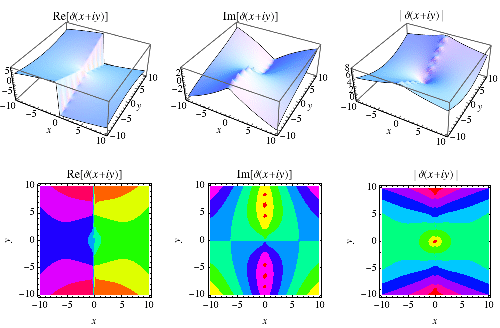 |
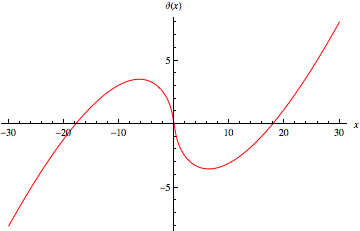
For real 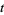 , the Riemann-Siegel theta function
, the Riemann-Siegel theta function 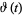 is defined as
is defined as
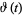 |
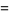 |
![I[lnGamma(1/4+1/2it)]-1/2tlnpi](http://mathworld.wolfram.com/images/equations/Riemann-SiegelFunctions/Inline11.gif) |
(2) |
 |
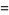 |
![arg[Gamma(1/4+1/2it)]-1/2tlnpi.](http://mathworld.wolfram.com/images/equations/Riemann-SiegelFunctions/Inline14.gif) |
(3) |
The function 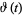 has local extrema at
has local extrema at 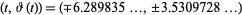 (OEIS A114865 and A114866).
(OEIS A114865 and A114866).
Values 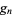 such that
such that
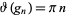 |
(4) |
for 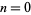 , 1, ... are known as Gram points (Edwards 2001, pp. 125-126).
, 1, ... are known as Gram points (Edwards 2001, pp. 125-126).
The series expansion of 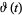 about 0 is given by
about 0 is given by
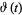 |
 |
 |
(5) |
 |
 |
![1/2[-lnpi+psi(1/4)]t-1/(48)psi_2(1/4)t^3+1/(3840)psi_4(1/4)t^5-1/(645120)psi_6(1/4)t^7](http://mathworld.wolfram.com/images/equations/Riemann-SiegelFunctions/Inline25.gif) |
(6) |
 |
 |
![-1/4[2gamma+pi+2ln(8pi)]t+1/(24)[pi^3+28zeta(3)]t^3-[(pi^5)/(96)+(31zeta(5))/(10)]+...](http://mathworld.wolfram.com/images/equations/Riemann-SiegelFunctions/Inline28.gif) |
(7) |
(OEIS A067626), and about  by
by
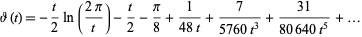 |
(8) |
(OEIS A036282 and A114721; Edwards 2001, p. 120).
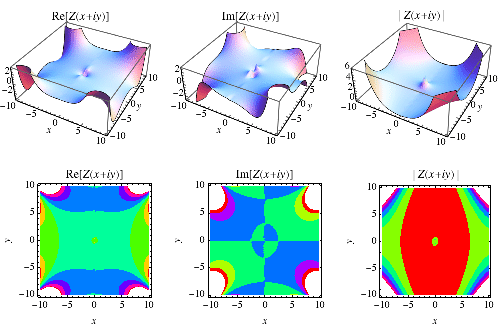
These functions are implemented in the Wolfram Language as RiemannSiegelZ[z] and RiemannSiegelTheta[z].
REFERENCES:
Berry, M. V. "The Riemann-Siegel Expansion for the Zeta Function: High Orders and Remainders." Proc. Roy. Soc. London A 450, 439-462, 1995.
Borwein, J. M.; Bradley, D. M.; and Crandall, R. E. "Computational Strategies for the Riemann Zeta Function." J. Comput. Appl. Math. 121, 247-296, 2000.
Brent, R. P. "On the Zeros of the Riemann Zeta Function in the Critical Strip." Math. Comput. 33, 1361-1372, 1979.
Edwards, H. M. Riemann's Zeta Function. New York: Dover, 2001.
Karatsuba, A. A. and Voronin, S. M. The Riemann Zeta-Function. Hawthorn, NY: de Gruyter, 1992.
Odlyzko, A. M. "The 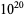 th Zero of the Riemann Zeta Function and 70 Million of Its Neighbors." Preprint.
th Zero of the Riemann Zeta Function and 70 Million of Its Neighbors." Preprint.
Sloane, N. J. A. Sequences A036282, A114721, A114865, and A114866 in "The On-Line Encyclopedia of Integer Sequences."
Titchmarsh, E. C. The Theory of the Riemann Zeta Function, 2nd ed. New York: Clarendon Press, 1987.
van de Lune, J.; te Riele, H. J. J.; and Winter, D. T. "On the Zeros of the Riemann Zeta Function in the Critical Strip. IV." Math. Comput. 46, 667-681, 1986.
Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, p. 143, 1991.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
قسم الحزام الأخضر الجنوبي ينظّم حفلاً بذكرى ولادة الإمام علي (عليه السلام)
|
|
|