المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Fine,s Equation |
 1904
 06:07 مساءً
date: 22-8-2019 |
Author : Andrews, G. E 
Book or Source : ercy Alexander MacMahon: Collected Papers, Vol. 2. Cambridge, MA: MIT Press, 
Page and Part : ...|
Read More
Date: 20-8-2018
1883
Date: 30-7-2019
1088
Date: 13-8-2018
1237
|
The q-series identity
 |
 |
 |
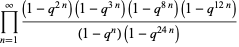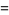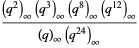(1) |
 |
 |
 |
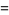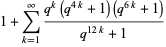(2) |
 |
 |
 |
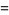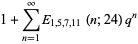(3) |
 |
 |
 |
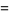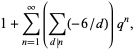(4) |
where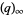 
is a q-Pochhammer symbol, 
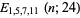is the number of divisors of 
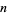that are congruent to 1, 5, 7, and 11
(mod 24) minus the number of divisors of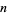 
congruent to 
, 
, 
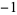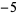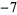, and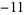 
(mod 24), and 
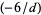is a Kronecker symbol.
REFERENCES:
Andrews, G. E. (Ed.). Percy Alexander MacMahon: Collected Papers, Vol. 2. Cambridge, MA: MIT Press, p. 260, 1986.
Andrews, G. E. "Nathan Fine, 1916-1994." Not. Amer. Math. Soc. 42, 678-679, 1995.
Sloane, N. J. A. Sequence A000377 in "The On-Line Encyclopedia of Integer Sequences."
|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
قسم الشؤون الفكرية يصدر كتاب الفلسفة الغربية برؤية الشيخ مرتضى مطهري
|
|
|
