المرجع الالكتروني للمعلوماتية
المرجع الألكتروني للمعلوماتية
ENGLISH
آخر المواضيع المضافة

الرياضيات
عدد المواضيع في هذا القسم 9761 موضوعاً
تاريخ الرياضيات
الرياضيات المتقطعة
الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
التحليل
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان

Untitled Document
أبحث عن شيء أخر المرجع الالكتروني للمعلوماتية
أضيف حديثاً
الشكر قناة موصلة للنعم الإلهية
2025-01-12
أسباب ودوافع الكفران وطرق علاجه
2025-01-12
عواقب كفران النعمة
2025-01-12
معنى كفران النعمة
2025-01-12
دور الإدارة الحكوميـة فـي التنـميـة التكـنولوجـيـة 2
2025-01-12
دور الإدارة الحكوميـة فـي التنـميـة التكـنولوجـيـة 1
2025-01-12

وثائقيات
العباءة العربية .. إرث الآباء واعتزاز الأبناء
التاريخ / 20-09-2024

مختارات
/X, M/
2024-02-14
The cubic close-packed structure
2-5-2020
مبررات تقييد الحقوق السياسية
25-6-2021
تكاثف النوفيناجيل
2023-08-01
الثايرستور الضوئي: LASCR
2023-08-21
مؤشرات التوتر وضغوط العمل الإعلامي
1-9-2020

q-Chu-Vandermonde Identity  
  
1123   07:03 مساءً   date: 26-8-2019
Author : Bhatnagar, G.
Book or Source : Inverse Relations, Generalized Bibasic Series, and their U(n) Extensions. Ph.D. thesis. Ohio State University,
Page and Part : ...


Read More
Montgomery-Odlyzko Law
Date: 9-9-2019 1475
Nu Function
Date: 23-5-2019 1748
Exponential Decay
Date: 2-5-2019 1600

q-Chu-Vandermonde Identity

A q-analog of the Chu-Vandermonde identity given by

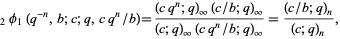_2phi_1(q^(-n),b;c;q,cq^n/b)=((cq^n;q)_infty(c/b;q)_infty)/((c;q)_infty(cq^n/b;q)_infty)=((c/b;q)_n)/((c;q)_n),

where 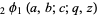_2phi_1(a,b;c;q,z) is the q-hypergeometric function. The identity can also be written as

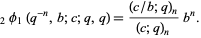_2phi_1(q^(-n),b;c;q,q)=((c/b;q)_n)/((c;q)_n)b^n.

REFERENCES:

Bhatnagar, G. Inverse Relations, Generalized Bibasic Series, and their U(n) Extensions. Ph.D. thesis. Ohio State University, p. 18, 1995.

Gasper, G. and Rahman, M. Basic Hypergeometric Series. Cambridge, England: Cambridge University Press, p. 236, 1990.

Koepf, W. Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities. Braunschweig, Germany: Vieweg, p. 43, 1998.




الجبر أحد الفروع الرئيسية في الرياضيات، حيث إن التمكن من الرياضيات يعتمد على الفهم السليم للجبر. ويستخدم المهندسون والعلماء الجبر يومياً، وتعول المشاريع التجارية والصناعية على الجبر لحل الكثير من المعضلات التي تتعرض لها. ونظراً لأهمية الجبر في الحياة العصرية فإنه يدرّس في المدارس والجامعات في جميع أنحاء العالم. ويُعجب الكثير من الدارسين للجبر بقدرته وفائدته الكبيرتين، إذ باستخدام الجبر يمكن للمرء أن يحل كثيرًا من المسائل التي يتعذر حلها باستخدام الحساب فقط.وجاء اسمه من كتاب عالم الرياضيات والفلك والرحالة محمد بن موسى الخورازمي.


يعتبر علم المثلثات Trigonometry علماً عربياً ، فرياضيو العرب فضلوا علم المثلثات عن علم الفلك كأنهما علمين متداخلين ، ونظموه تنظيماً فيه لكثير من الدقة ، وقد كان اليونان يستعملون وتر CORDE ضعف القوسي قياس الزوايا ، فاستعاض رياضيو العرب عن الوتر بالجيب SINUS فأنت هذه الاستعاضة إلى تسهيل كثير من الاعمال الرياضية.

تعتبر المعادلات التفاضلية خير وسيلة لوصف معظم المـسائل الهندسـية والرياضـية والعلمية على حد سواء، إذ يتضح ذلك جليا في وصف عمليات انتقال الحرارة، جريان الموائـع، الحركة الموجية، الدوائر الإلكترونية فضلاً عن استخدامها في مسائل الهياكل الإنشائية والوصف الرياضي للتفاعلات الكيميائية.
ففي في الرياضيات, يطلق اسم المعادلات التفاضلية على المعادلات التي تحوي مشتقات و تفاضلات لبعض الدوال الرياضية و تظهر فيها بشكل متغيرات المعادلة . و يكون الهدف من حل هذه المعادلات هو إيجاد هذه الدوال الرياضية التي تحقق مشتقات هذه المعادلات.





الأخبار الصحية
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
التاريخ / 2025-01-12

الأخبار العلمية
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
التاريخ / 2025-01-12

الساحة الاسلامية
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
التاريخ / 2025-01-12