


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 8-9-2019
Date: 21-9-2018
Date: 19-7-2019
|
The symbol ![RadicalBox[x, n]](http://mathworld.wolfram.com/images/equations/Radical/Inline1.gif) used to indicate a root is called a radical, or sometimes a surd. The expression
used to indicate a root is called a radical, or sometimes a surd. The expression ![RadicalBox[x, n]](http://mathworld.wolfram.com/images/equations/Radical/Inline2.gif) is therefore read "
is therefore read " radical
radical 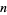 ," or "the nth root of
," or "the nth root of  ." In the radical symbol, the horizonal line is called the vinculum, the quantity under the vinculum is called the radicand, and the quantity
." In the radical symbol, the horizonal line is called the vinculum, the quantity under the vinculum is called the radicand, and the quantity 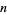 written to the left is called the index.
written to the left is called the index.
In general, the use of roots is equivalent to the use of fractional exponents as indicated by the identity
![(RadicalBox[x, p])^q=x^(p/q),](http://mathworld.wolfram.com/images/equations/Radical/NumberedEquation1.gif) |
(1) |
a more generalized form of the standard
![RadicalBox[x, n]=x^(1/n).](http://mathworld.wolfram.com/images/equations/Radical/NumberedEquation2.gif) |
(2) |
The special case ![RadicalBox[x, 2]](http://mathworld.wolfram.com/images/equations/Radical/Inline7.gif) is written
is written 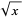 and is called the square root of
and is called the square root of  .
. ![RadicalBox[x, 3]](http://mathworld.wolfram.com/images/equations/Radical/Inline10.gif) is called the cube root.
is called the cube root.
Some interesting radical identities are due to Ramanujan, and include the equivalent forms
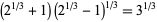 |
(3) |
and
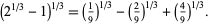 |
(4) |
Another such identity is
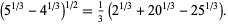 |
(5) |
REFERENCES:
Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 1168, 2002.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|