
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-9-2019
Date: 23-4-2019
Date: 19-7-2019
|
Polynomials 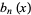 which form a Sheffer sequence with
which form a Sheffer sequence with
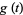 |
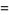 |
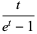 |
(1) |
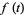 |
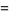 |
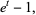 |
(2) |
giving generating function
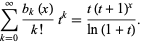 |
(3) |
Roman (1984) defines Bernoulli numbers of the second kind as 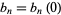 . They are related to the Stirling numbers of the first kind
. They are related to the Stirling numbers of the first kind 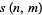 by
by
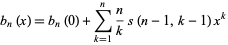 |
(4) |
(Roman 1984, p. 115), and obey the reflection formula
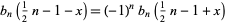 |
(5) |
(Roman 1984, p. 119).
The first few Bernoulli polynomials of the second kind are
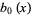 |
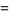 |
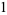 |
(6) |
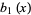 |
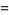 |
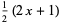 |
(7) |
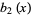 |
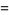 |
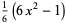 |
(8) |
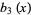 |
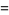 |
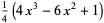 |
(9) |
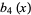 |
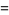 |
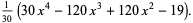 |
(10) |
REFERENCES:
Roman, S. "The Bernoulli Polynomials of the Second Kind." §5.3.2 in The Umbral Calculus. New York: Academic Press, pp. 113-119, 1984.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|