


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 15-1-2020
Date: 29-12-2020
Date: 25-12-2020
|
Given a hereditary representation of a number 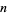 in base
in base 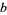 , let
, let ](http://mathworld.wolfram.com/images/equations/GoodsteinSequence/Inline3.gif) be the nonnegative integer which results if we syntactically replace each
be the nonnegative integer which results if we syntactically replace each 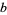 by
by 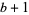 (i.e.,
(i.e., ![B[b]](http://mathworld.wolfram.com/images/equations/GoodsteinSequence/Inline6.gif) is a base change operator that 'bumps the base' from
is a base change operator that 'bumps the base' from 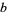 up to
up to 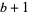 ). The hereditary representation of 266 in base 2 is
). The hereditary representation of 266 in base 2 is
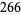 |
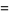 |
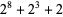 |
(1) |
 |
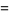 |
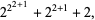 |
(2) |
so bumping the base from 2 to 3 yields
=3^(3^(3+1))+3^(3+1)+3.](http://mathworld.wolfram.com/images/equations/GoodsteinSequence/NumberedEquation1.gif) |
(3) |
Now repeatedly bump the base and subtract 1,
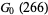 |
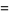 |
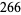 |
(4) |
 |
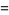 |
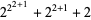 |
(5) |
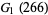 |
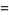 |
-1=3^(3^(3+1))+3^(3+1)+2](http://mathworld.wolfram.com/images/equations/GoodsteinSequence/Inline23.gif) |
(6) |
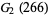 |
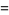 |
-1=4^(4^(4+1))+4^(4+1)+1](http://mathworld.wolfram.com/images/equations/GoodsteinSequence/Inline26.gif) |
(7) |
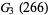 |
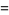 |
-1=5^(5^(5+1))+5^(5+1)](http://mathworld.wolfram.com/images/equations/GoodsteinSequence/Inline29.gif) |
(8) |
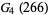 |
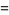 |
-1=6^(6^(6+1))+6^(6+1)-1](http://mathworld.wolfram.com/images/equations/GoodsteinSequence/Inline32.gif) |
(9) |
 |
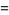 |
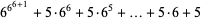 |
(10) |
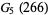 |
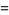 |
-1](http://mathworld.wolfram.com/images/equations/GoodsteinSequence/Inline38.gif) |
(11) |
 |
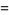 |
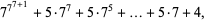 |
(12) |
etc.
Starting this procedure at an integer 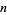 gives the Goodstein sequence
gives the Goodstein sequence 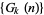 . Amazingly, despite the apparent rapid increase in the terms of the sequence, Goodstein's theorem states that
. Amazingly, despite the apparent rapid increase in the terms of the sequence, Goodstein's theorem states that 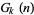 is 0 for any
is 0 for any 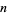 and any sufficiently large
and any sufficiently large 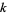 . Even more amazingly, Paris and Kirby showed in 1982 that Goodstein's theorem is not provable in ordinary Peano arithmetic (Borwein and Bailey 2003, p. 35).
. Even more amazingly, Paris and Kirby showed in 1982 that Goodstein's theorem is not provable in ordinary Peano arithmetic (Borwein and Bailey 2003, p. 35).
REFERENCES:
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, pp. 34-35, 2003.
Goodstein, R. L. "On the Restricted Ordinal Theorem." J. Symb. Logic 9, 33-41, 1944.
Henle, J. M. An Outline of Set Theory. New York: Springer-Verlag, 1986.
Simpson, S. G. "Unprovable Theorems and Fast-Growing Functions." Contemp. Math. 65, 359-394, 1987.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|