


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-11-2020
Date: 22-9-2020
Date: 27-2-2020
|
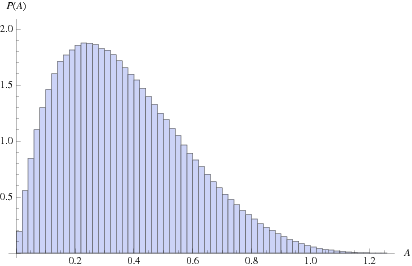
Ball triangle picking is the selection of triples of points (corresponding to vertices of a general triangle) randomly placed inside a ball.  random triangles can be picked in a unit ball in the Wolfram Language using the function RandomPoint[Ball[],
random triangles can be picked in a unit ball in the Wolfram Language using the function RandomPoint[Ball[],  n, 3
n, 3 ].
].
The distribution of areas of a triangle with vertices picked at random in a unit ball is illustrated above. The mean triangle area is
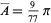 |
(1) |
(Buchta and Müller 1984, Finch 2010).
 random triangles can be picked in a unit ball in the Wolfram Language using the function RandomPoint[Ball[],
random triangles can be picked in a unit ball in the Wolfram Language using the function RandomPoint[Ball[], 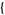 n, 3
n, 3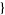 ].
].
The determination of the probability for obtaining an acute triangle by picking three points at random in the unit disk was generalized by Hall (1982) to the 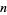 -dimensional ball. Buchta (1986) subsequently gave closed form evaluations for Hall's integrals. Let
-dimensional ball. Buchta (1986) subsequently gave closed form evaluations for Hall's integrals. Let 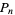 be the probability that three points chosen independently and uniformly from the
be the probability that three points chosen independently and uniformly from the 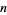 -ball form an acute triangle, then
-ball form an acute triangle, then
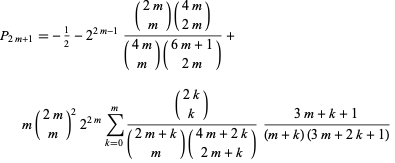 |
(2) |
![P_(2m+2)=1/4-3/(2^(2m+4))((4m+4; m+1))/((2m+2; m+1))+(2^(4m))/((2m; m)pi^2)[1/((2m+1)^2(2m; m))+sum_(k=0)^(m)(2^(2k)(3m+k-3))/((2k+1)(2k; k)(2m+k; m)(2m+k+2; 2))].](http://mathworld.wolfram.com/images/equations/BallTrianglePicking/Inline11.gif) |
(3) |
These can be combined and written in the slightly messy closed form
![P_n=pi^(-3/2){2^(2n-5)(n-1)[Gamma(1/2n)]^4[n_3F^~_2(1,n+1,1/2n+1;1/2(n+3),3/2n+1;1)-2_3F^~_2(1,n,1/2n+1;3/2n,1/2(n+3);1)]
-(sqrt(pi)Gamma(2n))/(4^nGamma(3/2n)Gamma(1/2(n+1)))+1},](http://mathworld.wolfram.com/images/equations/BallTrianglePicking/NumberedEquation2.gif) |
(4) |
where 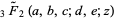 is a regularized hypergeometric function.
is a regularized hypergeometric function.
The first few are
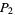 |
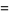 |
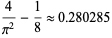 |
(5) |
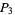 |
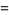 |
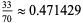 |
(6) |
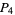 |
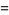 |
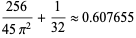 |
(7) |
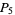 |
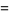 |
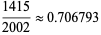 |
(8) |
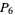 |
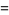 |
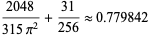 |
(9) |
 |
 |
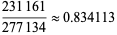 |
(10) |
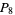 |
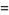 |
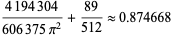 |
(11) |
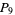 |
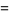 |
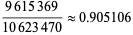 |
(12) |
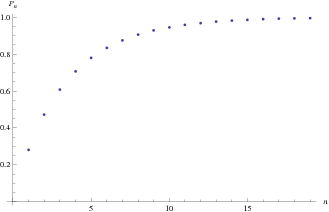
(OEIS A093756 and A093757, OEIS A093758 and A093759, and OEIS A093760 and A093761), plotted above.
The case 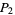 corresponds to disk triangle picking.
corresponds to disk triangle picking.
REFERENCES:
Buchta, C. "A Note on the Volume of a Random Polytope in a Tetrahedron." Ill. J. Math. 30, 653-659, 1986.
Buchta, C. and Müller, J. "Random Polytopes in a Ball." J. Appl. Prob. 21, 753-762, 1984.
Finch, S. "Random Triangles III." http://algo.inria.fr/csolve/rtg3.pdf. Apr. 30, 2010.
Hall, G. R. "Acute Triangles in the 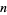 -Ball." J. Appl. Prob. 19, 712-715, 1982.
-Ball." J. Appl. Prob. 19, 712-715, 1982.
Sloane, N. J. A. Sequences A093756, A093757, A093758, A093759, A093760, and A093761 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
العتبة العباسية تستعدّ لتكريم عددٍ من الطالبات المرتديات للعباءة الزينبية في جامعات كركوك
|
|
|