


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 14-7-2020
Date: 7-11-2020
Date: 27-9-2020
|

Given four points chosen at random inside a unit cube, the average volume of the tetrahedron determined by these points is given by
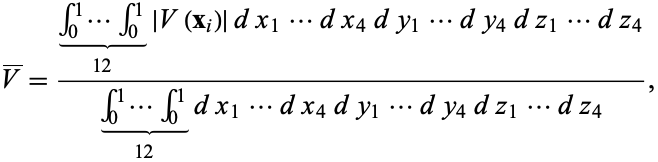 |
(1) |
where the polyhedron vertices are located at 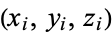 where
where 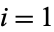 , ..., 4, and the (signed) volume is given by the determinant
, ..., 4, and the (signed) volume is given by the determinant
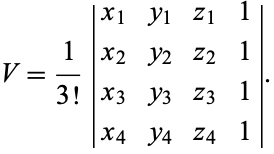 |
(2) |
The integral is extremely difficult to compute, but the analytic result for the mean tetrahedron volume is
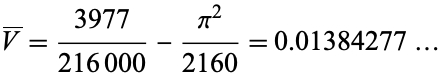 |
(3) |
(OEIS A093524; Zinani 2003). Note that the result quoted in the reply to Seidov (2000) actually refers to the average volume for tetrahedron tetrahedron picking.
REFERENCES:
Do, K.-A. and Solomon, H. "A Simulation Study of Sylvester's Problem in Three Dimensions." J. Appl. Prob. 23, 509-513, 1986.
Seidov, Z. F. "Letters: Random Triangle." Mathematica J. 7, 414, 2000.
Sloane, N. J. A. Sequence A093524 in "The On-Line Encyclopedia of Integer Sequences."
Zinani, A. "The Expected Volume of a Tetrahedron Whose Vertices are Chosen at Random in the Interior of a Cube." Monatshefte Math. 139, 341-348, 2003.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|