المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Digit-Shifting Constants |
 758
 05:24 مساءً
date: 23-2-2020 |
Author : المرجع الالكتروني للمعلوماتيه 
Book or Source : المرجع الالكتروني للمعلوماتيه 
Page and Part : ...|
Read More
Date: 20-10-2019
893
Date: 6-12-2020
606
Date: 24-4-2020
757
|
Given a real number 
, find the powers of a base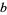 
that will shift the digits of 
a number of places 
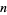to the left. This is equivalent to solving
 |
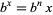(1) |
or
 |
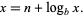(2) |
The solution is given by
 |
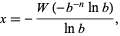(3) |
where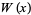 
is the Lambert W-function.
The above plot shows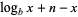 
for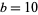 
and small values of 
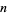. As can be seen, there are two distinct solutions, corresponding to two different branches of 
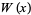in (3). For 
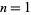, 2, ..., these solutions are approximately given by 0.137129, 0.0102386, 0.00100231, 0.000100023, 0.0000100002, ..., and 1, 2.37581, 3.55026, 4.66925, 5.76046, ..., respectively. For example,
 |
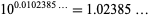(4) |
and
 |
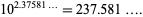(5) |
|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|
