


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-7-2020
Date: 4-1-2021
Date: 14-11-2019
|
The Copeland-Erdős constant has decimal expansion
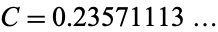 |
(OEIS A033308).
The Earls sequence (starting position of 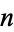 copies of the digit
copies of the digit 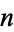 ) for
) for 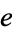 is given for
is given for 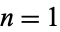 , 2, ... by 5, 113, 1181, 21670, 263423, 7815547, 35619942, ... (OEIS A224897).
, 2, ... by 5, 113, 1181, 21670, 263423, 7815547, 35619942, ... (OEIS A224897).
The digit sequences 0123456789 and 9876543210 do not occur in the first 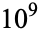 digits (E. Weisstein, Jul. 24, 2013).
digits (E. Weisstein, Jul. 24, 2013).
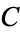 -constant primes occur at 1, 2, 4, 11, 353, 355, 499, 1171, 1543, 5719, 11048, 68433, 97855, 292447, ... (OEIS A227530) decimal digits. There are no others with fewer than
-constant primes occur at 1, 2, 4, 11, 353, 355, 499, 1171, 1543, 5719, 11048, 68433, 97855, 292447, ... (OEIS A227530) decimal digits. There are no others with fewer than 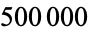 decimal digits (Rodenkirch, Jun. 18, 2016).
decimal digits (Rodenkirch, Jun. 18, 2016).
The starting positions of the first occurrence of 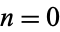 , 1, 2, ... in the decimal expansion of
, 1, 2, ... in the decimal expansion of 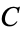 (not counting the initial 0 to the left of the decimal point) are 48, 5, 1, 2, 21, 3, 31, 4, 41, 12, ... (OEIS A229190).
(not counting the initial 0 to the left of the decimal point) are 48, 5, 1, 2, 21, 3, 31, 4, 41, 12, ... (OEIS A229190).
Scanning the decimal expansion of 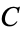 until all
until all 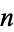 -digit numbers have occurred, the last 1-, 2-, ... digit numbers appearing are 0, 84, 504, 8580, 07010, 088880, ... (OEIS A000000), which end at digits 48, 934, 24437, 366399, 4910479, 49672582, ... (OEIS A000000).
-digit numbers have occurred, the last 1-, 2-, ... digit numbers appearing are 0, 84, 504, 8580, 07010, 088880, ... (OEIS A000000), which end at digits 48, 934, 24437, 366399, 4910479, 49672582, ... (OEIS A000000).
It is known that the Copeland-Erdős constant is normal in base 10 (Copeland and Erdős 1946), though the following table giving the counts of digits in the first 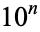 terms, shows non-normal behavior up to at least
terms, shows non-normal behavior up to at least 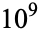 due arbitrarily cutting the digit string off in the middle of runs of primes with initial starting digits.
due arbitrarily cutting the digit string off in the middle of runs of primes with initial starting digits.
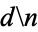 |
OEIS | 10 | 100 | 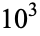 |
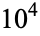 |
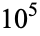 |
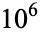 |
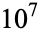 |
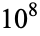 |
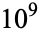 |
| 0 | A000000 | 0 | 4 | 46 | 575 | 6799 | 75249 | 790407 | 8129359 | 83121745 |
| 1 | A000000 | 4 | 33 | 266 | 2301 | 20468 | 187375 | 1766602 | 16794379 | 161034016 |
| 2 | A000000 | 1 | 4 | 63 | 731 | 8016 | 84314 | 876083 | 9016914 | 91679602 |
| 3 | A000000 | 2 | 16 | 134 | 1259 | 12015 | 115987 | 1134513 | 11201736 | 110467722 |
| 4 | A000000 | 0 | 4 | 60 | 685 | 7286 | 76925 | 796194 | 8202026 | 83946253 |
| 5 | A000000 | 1 | 5 | 58 | 674 | 7346 | 76886 | 794905 | 8161691 | 83863547 |
| 6 | A000000 | 0 | 4 | 60 | 667 | 7247 | 76745 | 794002 | 8154232 | 83381734 |
| 7 | A000000 | 2 | 16 | 133 | 1228 | 11889 | 115336 | 1129053 | 11107597 | 109702515 |
| 8 | A000000 | 0 | 3 | 57 | 654 | 7107 | 76273 | 791955 | 8141173 | 83207903 |
| 9 | A000000 | 0 | 11 | 123 | 1226 | 11827 | 114910 | 1126286 | 11090893 | 109594963 |
REFERENCES:
Copeland, A. H. and Erdős, P. "Note on Normal Numbers." Bull. Amer. Math. Soc. 52, 857-860, 1946.
Rodenkirch, M. "Copeland-Erdos Constant Primes." May. 5, 2016. http://www.mersenneforum.org/showthread.php?p=433145#post433145.
Sloane, N. J. A. Sequences A224897, A227530, and A229190 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
دراسة: حفنة من الجوز يوميا تحميك من سرطان القولون
|
|
|
|
|
|
|
تنشيط أول مفاعل ملح منصهر يستعمل الثوريوم في العالم.. سباق "الأرنب والسلحفاة"
|
|
|
|
|
|
|
سماحة السيد الصافي: السيد أحمد الإشكوري حجّةٌ على كلّ طالب علمٍ في عمره وإخلاصه وجهده
|
|
|