Mills' Constant

Mills' theorem states that there exists a real constant 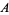 such that  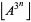is prime for all positive integers  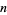(Mills 1947). While for each value of 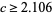, there are uncountably many possible values of  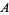such that  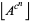is prime for all positive integers  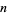(Caldwell and Cheng 2005), it is possible to define Mills' constant as the least  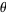such that

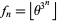is prime for all positive integers 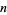, giving a value of

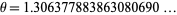(OEIS A051021).

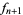 is therefore given by the next prime after 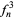, and the values of  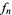are known as Mills' primes (Caldwell and Cheng 2005).

Caldwell and Cheng (2005) computed more than 6850 digits of 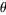 assuming the truth of the Riemann hypothesis. Proof of primality of the 13 Mills prime in Jul. 2013 means that approximately  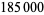digits are now known.

It is not known if 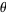 is irrational.

REFERENCES:

Caldwell, C. K. and Cheng, Y. "Determining Mills' Constant and a Note on Honaker's Problem." J. Integer Sequences 8, Article 05.4.1, 1-9, 2005. http://www.cs.uwaterloo.ca/journals/JIS/VOL8/Caldwell/caldwell78.html.

Finch, S. R. "Mills' Constant." §2.13 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 130-133, 2003.

Mills, W. H. "A Prime-Representing Function." Bull. Amer. Math. Soc. 53, 604, 1947.

Ribenboim, P. The Little Book of Big Primes. New York: Springer-Verlag, pp. 109-110, 1991.

Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, pp. 186-187, 1996.

Sloane, N. J. A. Sequences A051021, A051254, and A108739 in "The On-Line Encyclopedia of Integer Sequences."