


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 17-8-2020
Date: 20-8-2020
Date: 12-11-2019
|
The Skewes number (or first Skewes number) is the number 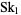 above which
above which 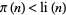 must fail (assuming that the Riemann hypothesis is true), where
must fail (assuming that the Riemann hypothesis is true), where 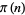 is the prime counting function and
is the prime counting function and 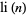 is the logarithmic integral.
is the logarithmic integral.
Isaac Asimov featured the Skewes number in his science fact article "Skewered!" (1974).
In 1912, Littlewood proved that 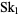 exists (Hardy 1999, p. 17), and the upper bound
exists (Hardy 1999, p. 17), and the upper bound
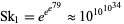 |
was subsequently found by Skewes (1933). The Skewes number has since been reduced to 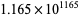 by Lehman in 1966 (Conway and Guy 1996; Derbyshire 2004, p. 237),
by Lehman in 1966 (Conway and Guy 1996; Derbyshire 2004, p. 237), 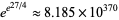 by te Riele (1987), and less than
by te Riele (1987), and less than 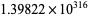 (Bays and Hudson 2000; Granville 2002; Borwein and Bailey 2003, p. 65; Havil 2003, p. 200; Derbyshire 2004, p. 237). The results of Bays and Hudson left open the possibility that the inequality could fail around
(Bays and Hudson 2000; Granville 2002; Borwein and Bailey 2003, p. 65; Havil 2003, p. 200; Derbyshire 2004, p. 237). The results of Bays and Hudson left open the possibility that the inequality could fail around 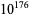 , and thus established a large range of violation around
, and thus established a large range of violation around 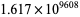 (Derbyshire 2004, p. 237). More recent work by Demichel establishes that the first crossover occurs around
(Derbyshire 2004, p. 237). More recent work by Demichel establishes that the first crossover occurs around 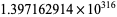 , where the probability that another crossover occurs before this value is infinitesimal and can in fact be dramatically reduced in the suspect regions where there is such a risk and these results are almost certainly the best currently possible (P. Demichel, pers. comm., Aug. 22, 2005).
, where the probability that another crossover occurs before this value is infinitesimal and can in fact be dramatically reduced in the suspect regions where there is such a risk and these results are almost certainly the best currently possible (P. Demichel, pers. comm., Aug. 22, 2005).
Rigorously, Rosser and Schoenfeld (1962) proved that there are no crossovers below 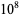 , and this lower bound was subsequently improved to
, and this lower bound was subsequently improved to 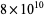 by Brent (1975) and to
by Brent (1975) and to 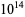 by Kotnik (2008).
by Kotnik (2008).
In 1914, Littlewood proved that the inequality must, in fact, fail infinitely often.
The second Skewes number 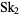 (Skewes 1955) is the number above which
(Skewes 1955) is the number above which 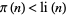 must fail assuming that the Riemann hypothesis is false. It is much larger than the Skewes number
must fail assuming that the Riemann hypothesis is false. It is much larger than the Skewes number 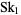 ,
,
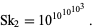 |
REFERENCES:
Asimov, I. "Skewered!" Of Matters Great and Small. New York: Ace Books, 1976.
Asimov, I. "Science: Skewered!" Mag. Fantasy Sci. Fiction. Nov. 1974.
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 63, 1987.
Bays, C. and Hudson, R. H. "A New Bound for the Smallest  with
with 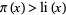 ." Math. Comput. 69, 1285-1296, 2000.
." Math. Comput. 69, 1285-1296, 2000.
Boas, R. P. "The Skewes Number." In Mathematical Plums (Ed. R. Honsberger). Washington, DC: Math. Assoc. Amer., 1979.
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, p. 65, 2003.
Brent, R. P. "Irregularities in the Distribution of Primes and Twin Primes." Math. Comput. 29, 43-56, 1975.
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, p. 61, 1996.
Crandall, R. and Pomerance, C. Ex. 1.35 in Prime Numbers: A Computational Perspective. New York: Springer-Verlag, 2001.
Demichel, P. "The Prime Counting Function and Related Subjects." http://demichel.net/patrick/li_crossover_pi.pdf.
Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, p. 236, 2004.
Granville, A. "Prime Possibilities and Quantum Chaos." 2002. http://www.msri.org/ext/Emissary/EmissarySpring02.pdf.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, pp. 17 and 21, 1999.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 200 and 209, 2003.
Kotnik, T. "The Prime-counting Function and its Analytic Approximations." Adv. Comput. Math. 29, 55-70, 2008.
Lehman, R. S. "On the Difference 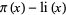 ." Acta Arith. 11, 397-410, 1966.
." Acta Arith. 11, 397-410, 1966.
Littlewood, J. E. Littlewood's Miscellany. Cambridge, England: Cambridge University Press, pp. 110-112, 1986.
Rosser, J. B. and Schoenfeld, L. "Approximate Formulas for some Functions of Prime Numbers." Ill. J. Math. 6, 64-94, 1962.
Skewes, S. "On the Difference 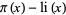 ." J. London Math. Soc. 8, 277-283, 1933.
." J. London Math. Soc. 8, 277-283, 1933.
Skewes, S. "On the Difference 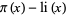 . II." Proc. London Math. Soc. 5, 48-70, 1955.
. II." Proc. London Math. Soc. 5, 48-70, 1955.
te Riele, H. J. J. "On the Sign of the Difference  ." Math. Comput. 48, 323-328, 1987.
." Math. Comput. 48, 323-328, 1987.
Wagon, S. Mathematica in Action. New York: W. H. Freeman, p. 30, 1991.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|