


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 24-4-2020
Date: 9-6-2020
Date: 24-11-2020
|
The 9.1.2 equation
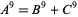 |
(1) |
is a special case of Fermat's last theorem with 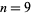 , and so has no solution. No 9.1.3, 9.1.4, 9.1.5, 9.1.6, 9.1.7, 9.1.8, or 9.1.9 solutions are known. A 9.1.10 solution is
, and so has no solution. No 9.1.3, 9.1.4, 9.1.5, 9.1.6, 9.1.7, 9.1.8, or 9.1.9 solutions are known. A 9.1.10 solution is
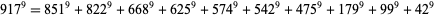 |
(2) |
(J. Wroblewski 2002), and two 9.1.11 solutions are given by
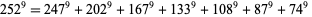 |
(3) |
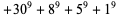 |
(4) |
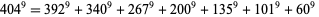 |
(5) |
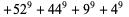 |
(6) |
(S. Chase; Aloril 2002). The smallest 9.1.12 solution is
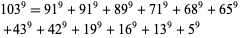 |
(7) |
(Meyrignac 1997). No 9.1.13 solution is known. The smallest 9.1.14 solution is
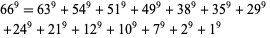 |
(8) |
(Ekl 1998).
No 9.2.2, 9.2.3, 9.2.4,. 9.2.5, 9.2.6, 9.2.7, or 9.2.8 solutions are known. 9.2.9 solutions include
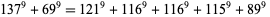 |
(9) |
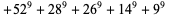 |
(10) |
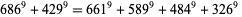 |
(11) |
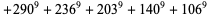 |
(12) |
(J. Wroblewski 2002). A 9.2.10 solution is given by
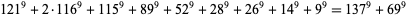 |
(13) |
(L. Morelli 1999). No 9.2.11 solutions are known. The smallest 9.2.12 solution is
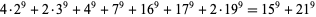 |
(14) |
(Lander et al. 1967, Ekl 1998). There are no known 9.2.13 or 9.2.14 solutions. The smallest 9.2.15 solution is
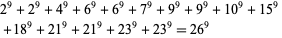 |
(15) |
(Lander et al. 1967).
There are no known 9.3.3, 9.3.4, 9.3.5, 9.3.6, 9.3.7, or 9.3.8 solutions. The smallest 9.3.9 solution is
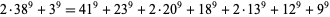 |
(16) |
(Ekl 1998). There is no known 9.3.10 solution. The smallest 9.3.11 solution is
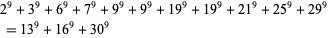 |
(17) |
(Lander et al. 1967).
No 9.4.4 or 9.4.5 solutions are known. The smallest 9.4.6 solution is
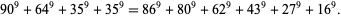 |
(18) |
There are no known 9.4.7 or 9.4.8 solutions. The smallest 9.4.9 solution is
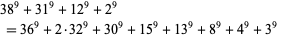 |
(19) |
(Ekl 1998). The smallest 9.4.10 solutions are
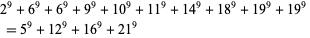 |
(20) |
(Lander et al. 1967).
The smallest 9.5.5 solution is
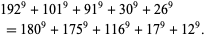 |
(21) |
There is no known 9.5.6 solution. The smallest 9.5.7 solution is
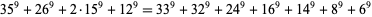 |
(22) |
(Ekl 1998). There are no known 9.5.8, 9.5.9, or 9.5.10 solutions. The smallest 9.5.11 solution is
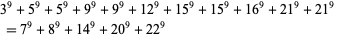 |
(23) |
(Lander et al. 1967).
The smallest 9.6.6 solutions are
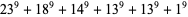 |
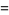 |
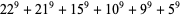 |
(24) |
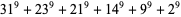 |
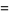 |
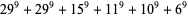 |
(25) |
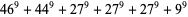 |
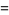 |
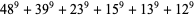 |
(26) |
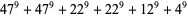 |
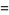 |
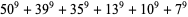 |
(27) |
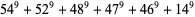 |
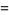 |
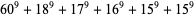 |
(28) |
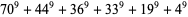 |
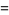 |
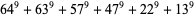 |
(29) |
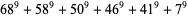 |
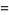 |
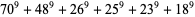 |
(30) |
(Lander et al. 1967, Ekl 1998).
Ekl (1998) mentions but does not list nine primitive solutions to the 9.7.7 equation.
Moessner (1947) gives a parametric solution to the 9.10.10 equation.
Palamá (1953) gave a solution to the 9.11.11 equation.
Moessner and Gloden (1944) give the 9.11.12 solution
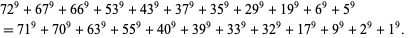 |
(31) |
REFERENCES:
Ekl, R. L. "New Results in Equal Sums of Like Powers." Math. Comput. 67, 1309-1315, 1998.
Lander, L. J.; Parkin, T. R.; and Selfridge, J. L. "A Survey of Equal Sums of Like Powers." Math. Comput. 21, 446-459, 1967.
Meyrignac, J.-C. "Computing Minimal Equal Sums of Like Powers." https://euler.free.fr.
Moessner, A. "On Equal Sums of Like Powers." Math. Student 15, 83-88, 1947.
Moessner, A. and Gloden, A. "Einige Zahlentheoretische Untersuchungen und Resultate." Bull. Sci. École Polytech. de Timisoara 11, 196-219, 1944.
Palamá, G. "Diophantine Systems of the Type 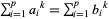 (
(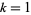 , 2, ...,
, 2, ..., 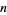 ,
, 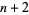 ,
, 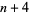 , ...,
, ..., 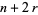 )." Scripta Math. 19, 132-134, 1953.
)." Scripta Math. 19, 132-134, 1953.



|
|
|
|
مقاومة الأنسولين.. أعراض خفية ومضاعفات خطيرة
|
|
|
|
|
|
|
أمل جديد في علاج ألزهايمر.. اكتشاف إنزيم جديد يساهم في التدهور المعرفي ؟
|
|
|
|
|
|
|
العتبة العباسية المقدسة تقيم ندوة علمية عن روايات كتاب نهج البلاغة
|
|
|