


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 9-12-2020
Date: 4-5-2020
Date: 20-10-2019
|
A Pythagorean quadruple is a set of positive integers 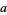 ,
, 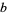 ,
, 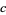 , and
, and 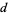 that satisfy
that satisfy
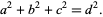 |
(1) |
For positive even 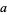 and
and 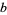 , there exist such integers
, there exist such integers 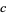 and
and 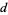 ; for positive odd
; for positive odd 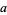 and
and 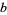 , no such integers exist (Oliverio 1996).
, no such integers exist (Oliverio 1996).
Examples of primitive Pythagorean quadruples include  ,
,  ,
,  ,
,  ,
,  , and
, and  .
.
Oliverio (1996) gives the following generalization of this result. Let 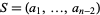 , where
, where 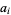 are integers, and let
are integers, and let 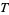 be the number of odd integers in
be the number of odd integers in 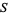 . Then iff
. Then iff 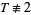 (mod 4), there exist integers
(mod 4), there exist integers 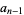 and
and 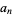 such that
such that
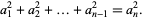 |
(2) |
A set of Pythagorean quadruples is given by
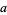 |
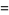 |
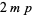 |
(3) |
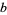 |
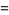 |
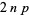 |
(4) |
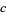 |
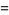 |
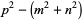 |
(5) |
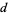 |
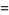 |
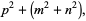 |
(6) |
where 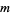 ,
, 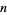 , and
, and 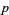 are integers (Mordell 1969). This does not, however, generate all solutions. For instance, it excludes (36, 8, 3, 37).
are integers (Mordell 1969). This does not, however, generate all solutions. For instance, it excludes (36, 8, 3, 37).
REFERENCES:
Carmichael, R. D. Diophantine Analysis. New York: Wiley, 1915.
Dutch, S. "Power Page: Pythagorean Quartets." https://www.uwgb.edu/dutchs/RECMATH/rmpowers.htm#pythquart.
Mordell, L. J. Diophantine Equations. London: Academic Press, 1969.
Oliverio, P. "Self-Generating Pythagorean Quadruples and 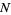 -tuples." Fib. Quart. 34, 98-101, 1996.
-tuples." Fib. Quart. 34, 98-101, 1996.



|
|
|
|
دراسة: حفنة من الجوز يوميا تحميك من سرطان القولون
|
|
|
|
|
|
|
تنشيط أول مفاعل ملح منصهر يستعمل الثوريوم في العالم.. سباق "الأرنب والسلحفاة"
|
|
|
|
|
|
|
لتعزيز التواصل مع الزائرات الأجنبيات : العتبة العلويّة المقدّسة تُطلق دورة لتعليم اللغة الإنجليزية لخادمات القسم النسويّ
|
|
|